Стійкість рівноваги
Під час проектування споруд, машин, різних пристроїв необхідно вибрати таке розташування опор і центрів мас, яке б забезпечувало рівновагу конструкції під дієш прикладених сил /баштові крани не перекидалися під дією вантажа чи вітру, греблі не руйнувалися під тиском вони, автомобілі не перекидалися під вантажем при повороті чи нахилі дороги тощо/.
Як відомо із фізики, тіло, яке має точку опори і на яке діє тільки сила ваги, знаходиться в рівновазі за умови, що сила ваги і реакція опори діють вздовж однієї прямої /друга аксіома статики/. При цьому розрізняють три види рівноваги: стійку, нестійку і байдужу.
|
За нестійкої рівноваги тіло, виведене з рівноваги, повертається в початкове положення. Прикладом стійкої рівноваги можуть служити куля, розміщена в сферичній чашці /рис. 17.15,а/ або підвішена на нитці /рис. 17.15, б/, тіло /шатун/, підвішене на призмі /рис. 17.І5,в/.У всіх цих випадках при виведенні тіла з рівноваги виникає сила 
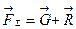або момент 
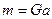,які повертають тіло в початкове положення, в якому 
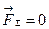або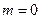 
, тобто 
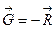. Отже, для забезпечення стійкої рівноваги тіла необхідно, щоб центр ваги займав найнижче положення і, якщо його вивести з рівноваги, то воно саме повертається в початкове положення. При нестійкій рівновазі тіло, виведене з рівноваги, не повертається в попереднє положення, а віддаляється від нього ще на більшу відстань. Прикладом нестійкої рівноваги можуть бути куля, розміщена в найвищій точці опуклої поверхні /рис. 17.16,а/, конус, поставлений на вершину /рис. 17.16,б/, кривошип, що закріплений шарнірно з опорою і знаходиться у верхньому положенні /рис. 17.16,в/ і т.ін. У всіх цих випадках тіла знаходяться в нестійкій рівновазі, тому що достатньо незначного зміщення їх із цього положення, щоб під дією не зрівноважених сил 
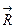і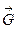 
вони стали віддалятися від верхнього положення. Причиною цього у першому випадку /рис. 17,16 ,а/ є сила 
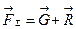,в інших - момент пари сил (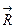 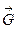),який дорівнює 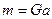.Отже, при нестійкій рівновазі центр ваги тіла займає найвище положення і при незначному відхиленні від положення рівноваги сам не повертається в початкове положення.
Можна вибрати точку опори тіла так, щоб незалежно від його положення рівновага не порушувалася. Зокрема, якщо опору важеля розмістити в центрі ваги /рис. 17.17,а/, то в будь-якому положенні важіль /кривошип/ вбереже рівновагу. Інший приклад зображений на рис. 17.17,б де циліндр /куля/ лежить на горизонтальній площині і за будь-якого відхилення від початкового положення зберігає стан рівноваги. Ці два приклади демонструють третій вид рівноваги - байдужої. Така рівновага має місце тоді, коли центр ваги не змінює свого положення за висотою, а сила ваги не створює при зміні положення тіла ніякого момента відносно точки опори.
Рис.17.17
Отже, рівновага називається байдужою, якщо положення центра ваги тіла за висотою відносно опори залишається незмінним.
На практиці найчастіше зустрічаються випадки, коли тіло спирається на опору не в одній точці, а має кілька таких точок стикання, які лежать не на одній прямій, тобто тіло має опорну поверхню /зокрема, площину/. Залежно від форми, розмірів площини, положення центра ваги відносно неї та величини і напряму діючих активних сил стійкість тіла може бути більшою або меншою, тобто піддається вимірюванню та кількісному порівнянню.
На рис. 17.18 зображено три положення тіла, яке має форму прямокутного паралелепіпеда /наприклад, цегла/. Не зважаючи на те, що в усіх трьох положеннях вага 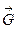тіла однакова, його стійкість буде різною і залежатиме від величини опорної поверхні й положення центра ваги тіла. У даному випадку найбільш стійкою рівновага буде в положенні, зображеному на рис. 7.18,в, коли опорна поверхня тіла найбільша, а центр ваги знаходиться на найменшій висоті.
Рис. 17.18
| |
| |
Якщо до тіла прикласти деяку силу
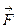як це показано на рис. 7.19,а, то за деякої величини цієї сили тіло почне повертатися навколо ребра А центр ваги С почне підніматися /рис. 7.19,б/, але якщо сила 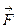перестане діяти, то тіло знову повернеться в початкове положення. Момент сили ваги може повертати тіло в попереднє положення рівноваги доти, доки лінія дії сили ваги 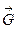проходитиме всередині площі опори. Граничний випадок буде тоді /рис. 7.19,в/, коли лінія дії сили ваги проходитиме через точку А /випадок нестійкої рівноваги/, тоді тіло утворює з горизонтальною площиною кут 
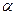, який називають кутом
Рис.17.19
стійкості тіла. Тобто це кут, на який необхідно повернути тіло, щоб воно під дією сили ваги не могло повернутися у попереднє положення рівноваги. Якщо кут повороту тіла буде більшим за кут 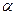, то тіло під дією своєї ваги не повертатиметься в початкове положення /рис. 7.19,г/.
Здатність тіл повертатися в початкове положення рівноваги після припинення дії сил, що порушують цю рівновагу, називають динамічною стійкістю. З наведених прикладів видно, що динамічна стійкість збільшується із збільшенням розмірів опорної поверхні і зниженням центра ваги. Проблема зберігання динамічної стійкості, як правило, виникає у процесі проектування, побудови й експлуатації кораблів, автомобілів, поїздів, літаків.
При зведенні будинків, монтажі верстатів та іншого промислового обладнання виникає проблема статичної стійкості. Статичною стійкістю називають здатність тіла створювати опір будь-якому малому порушенню рівноваги.
Як видно з рис. 7.19,а, сила 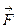намагається перекинути тіло. Момент цієї сили відносно ребра А називається перекидним і дорівнює 
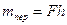. Сила 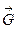навпаки, намагається зберегти або відновити стан рівноваги, тому її момент відносно ребра А називається моментом стійкості,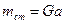 
Тіла /масиви/ зберігають статичну рівновагу поки зберігається нерівність
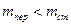/17.29/
Відношення абсолютних значень моментів стійкості і перекидного моменту
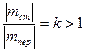/17.30/
називають коефіцієнтом стійкості.
Коефіцієнт стійкості к, який повинен бути більшим за одиницю, вказує на ступінь стійкості тіла. Величина коефіцієнтів к встановлюється нормами на проектування залежно від типу споруд, їх призначення, характеру навантаження та інших факторів
Питання для самоконтролю
- Що називають статичним моментом площі плоскої фігури відносно осі, як він обчислюється і яку розмірність має?
- Статичний момент плоскої фігури відносно осі Ох дорівнює нулю. Що можна сказати про центр ваги цієї фігури?
- Як визначити положення центра ваги площі, якщо відоме положення центрів ваги окремих її частин?
- Центри мас трьох однорідних дисків з однаковими масами розташовані у вершинах трикутника. Вкажіть положення центра мас системи.
- Центри мас чотирьох однорідних однакових за масою куль лежать у вершинах трикутної піраміди. Укажіть положення центра мас системи.
Заняття № 19
Тема:Центр тяжіння.
Лабораторна робота № 1. Визначення положення центру тяжіння плоских геометричних фігур.
Дата добавления: 2016-01-26; просмотров: 6380;