Векторний спосіб визначення швидкості і прискорення точки

При вектрному способі задання руху точки вважається відомим радіус-вектор точки як функція часу: .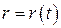

Швидкістю точки називається кінематична міра руху точки, яка дорівнює похідній за часом від радіуса-вектора цієї точки в обраній системі відліку

.

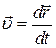(21.5)

З фізичної точки зору вектор швидкості визначає інтенсивність зміни просторового положення точки з часом. Напрямлений цей вектор по дотичній до траєкторії точки в бік її руху (рис. 21.3).

Розмірність швидкості 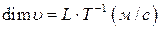(dimension – розмір, вимір).

Прискоренням точки називається кінематична міра зміни швидкості точки, яка дорівнює похідній за часом від швидкості цієї точки в обраній системі відліку

.

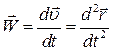(21.6)

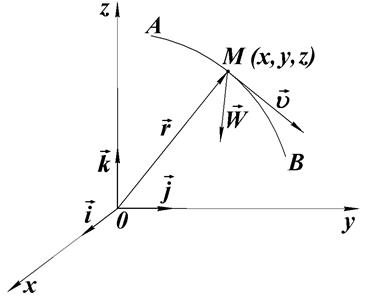
Рис. 21.3

Розмірність прискорення .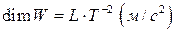

З рівняння (2.6) виходить, що прискорення точки дорівнює нулю тоді, коли швидкість точки зберігає сталу величину і сталий напрям, тобто 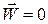при рівномірному прямолінійному русі точки. Напрям вектора 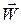співпадає з напрямом вектора 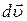– прирістом вектора швидкості за час .

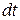Формули (21.5) і (21.6) зручно використовувати для теоретичного викладання кінематики точки, але для практичних обчислень їм надають більш конкретний вигляд.