Визначення швидкості і прискорення точки в декартовій системі координат

Загальні формули (21.5) і (21.6) визначають швидкість і прискорення точки через похідні за часом від її радіуса-вектора 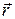, який через координати 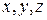точки (рис.22.2) можна записати так:

.

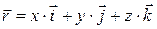Диференціюємо вираз за часом:

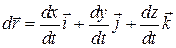
(22.3)

або

.

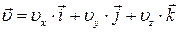(22.4)

Звідсіля виходить, що проекція швидкості точки на координатну вісь дорівнює першій похідній від відповідної координати точки за часом:

,

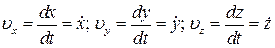(22.5)

де крапка над координатою – символ диференціювання за часом.

Модуль швидкості знаходимо за формулою

,

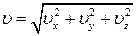(22.6)

а її напрям визначається напрямляючими косинусами:

.

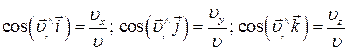(22.6')

Для визначення прискорення точки згідно з формулою (22.2) потрібно продиференціювати за часом співвідношення (22.3) і (22.4). Отримаємо

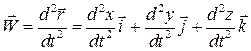
і

.

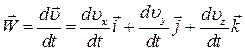З другого боку

.

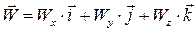З наведених рівнянь виходить, що проекції прискорення точки на координатні осі дорівнюють першим похідним від проекцій швидкості або другим похідним від відповідних координат точки за часом:

.

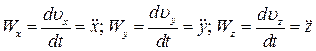(22.7)

Модуль прискорення знаходять за формулою

,

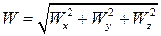(22.8)

а напрям визначають напрямляючі косинуси:

.

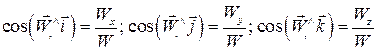(2.8')

З викладеного випливає, що залежності 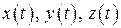по суті повністю визначають рух точки. Вони дають змогу знайти не тільки положення точки, але і проекції її швидкості і прискорення, а отже, модуль і напрям векторів 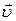і в будь-який момент часу. Крім того, можна розв’язати і ряд інших питань: знайти траєкторію точки, залежність швидкості від положення точки, тощо.

Розв’язання оберненої задачі – визначення швидкості і закону руху точки по заданому прискоренню – проводиться шляхом інтегрування проекцій прискорення за часом, причому задача буде мати однозначний розв’язок, якщо крім прискорення задані ще і початкові умови – проекції швидкості і координати точки в початковий момент часу.

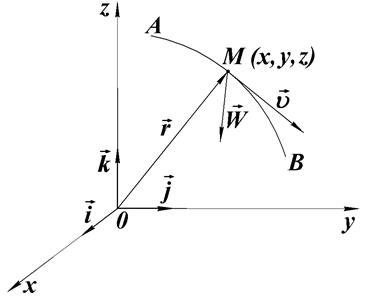
Рис.22.2

Питання для самоконтролю

1. Що називають траєкторією точки?
2. Які способи задання руху точки існують і в чому полягає кожний з них?
3. Чому функці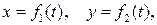ї і 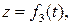що визначають рух точки в координатній формі, повинні бути однозначними?
4. Як при координатному способі задання руху точки визначається її траєкторія?
5. Чому дорівнює і як напрямлений у просторі вектор швидкості?
6. Чому дорівнюють проекції швидкості точки на осі нерухомої декартової системи координат?
7. Чому дорівнюють проекції швидкості точки на дотичну і головну нормаль до траєкторії?
8. Як за проекціями швидкості знайти її величину і напрям?
9. Чому дорівнює і як напрямлений у просторі вектор прискорення точки?
10. Як визначаються проекції прискорення точки на нерухомі осі декартової системи координат?
11. Як за проекціями прискорення знайти його модуль і напрям?
12. Що являє собою натуральна система координат; де знаходиться її початок і як напрямлені осі цієї системи?
13. Як визначаються проекції прискорення точки на осі натуральної системи координат ?
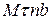14. Чи правильним є вираз для тангенціального прискорення :
15. ?

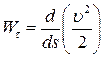Заняття 23