Обертальний рух твердого тіла навколо нерухомої осі. Обертальним рухом твердого тіла навколо нерухомої осі називають такий рух, при якому всі точки, що лежать на певній прямій
Обертальним рухом твердого тіла навколо нерухомої осі називають такий рух, при якому всі точки, що лежать на певній прямій, незмінно зв’язаній з тілом, залишаються нерухомими в обраній системі відліку.
Нерухому пряму, навколо якої обертається тіло, називають віссю обертання. Всі точки тіла, що не лежать на осі обертання, рухаються в площинах, перпендикулярних до осі обертання, і описують кола, центри яких знаходяться на цій осі. Відстань точки від осі обертання називають радіусом обертання точки.
Доцільно також відмітити, що всі прямі, проведені в тілі паралельно осі обертання, рухаються поступально.
Оберемо нерухому систему координат 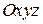 так, щоб вісь
так, щоб вісь 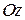 співпала з віссю обертання твердого тіла. Положення тіла, яке обертається навколо нерухомої осі, може бути визначено двогранним кутом
співпала з віссю обертання твердого тіла. Положення тіла, яке обертається навколо нерухомої осі, може бути визначено двогранним кутом 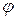 , котрий відлічують від певної нерухомої півплощини І до рухомої півплощини ІІ, що незмінно зв’язана з тілом (рис.23.4). Кут
, котрий відлічують від певної нерухомої півплощини І до рухомої півплощини ІІ, що незмінно зв’язана з тілом (рис.23.4). Кут 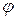 вважається додатним, якщо він відлічується від нерухомої півплощини в напрямку проти руху годинникової стрілки для спостерігача, що дивиться з додатного кінця осі
вважається додатним, якщо він відлічується від нерухомої півплощини в напрямку проти руху годинникової стрілки для спостерігача, що дивиться з додатного кінця осі 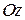 , і від’ємним, якщо він відрахований за рухом годинникової стрілки. Вимірюється кут
, і від’ємним, якщо він відрахований за рухом годинникової стрілки. Вимірюється кут 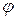 в радіанах (
в радіанах (  ).
).

Рис. 23.4
Рівняння
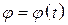 , ,
| (23.2) |
що установлює залежність кута 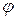 від часу, називають законом обертального руху тіла навколо нерухомої осі.
від часу, називають законом обертального руху тіла навколо нерухомої осі.
Для характеристики обертального руху використовують поняття кутової швидкості і кутового прискорення.
Кутова швидкість характеризує зміну з часом кута повороту тіла, а її алгебраїчна величина дорівнює першій похідній за часом від кута повороту:
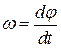 , або , або 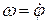 . .
| (23.3) |
Розмірність кутової швидкості 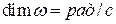 .
.
Знак 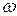 визначає напрям обертання: якщо обертання тіла відбувається проти руху годинникової стрілки, то
визначає напрям обертання: якщо обертання тіла відбувається проти руху годинникової стрілки, то 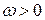 , якщо тіло обертається за рухом годинникової стрілки –
, якщо тіло обертається за рухом годинникової стрілки – 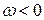 . Ця обставина відображується на рисунках (кресленнях) показом кутової швидкості за допомогою дугової стрілки.
. Ця обставина відображується на рисунках (кресленнях) показом кутової швидкості за допомогою дугової стрілки.
В техніці кутову швидкість часто задають числом обертів за хвилину 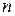 Оскільки за один оберт тіло повертається на кут
Оскільки за один оберт тіло повертається на кут 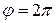 , то
, то
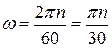 . .
| (23.4) |
Кутове прискоренняхарактеризує зміну з часом кутової швидкості тіла, а його алгебраїчна величина дорівнює першій похідній від кутової швидкості, або другій похідній від кута повороту тіла за часом
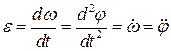 . .
| (23.5) |
Розмірність кутового прискорення dim 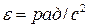 .
.
При обертанні твердого тіла навколо нерухомої осі можливі такі випадки:
о– при 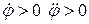 – тіло обертається прискорено в додатному напрямі (проти руху годинникової стрілки);
– тіло обертається прискорено в додатному напрямі (проти руху годинникової стрілки);
– при 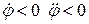 – тіло обертається прискорено у від’ємному напрямі (за рухом годинникової стрілки);
– тіло обертається прискорено у від’ємному напрямі (за рухом годинникової стрілки);
– при 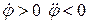 – сповільнене обертання в додатному напрямі;
– сповільнене обертання в додатному напрямі;
– при 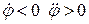 – сповільнене обертання у від’ємному напрямі.
– сповільнене обертання у від’ємному напрямі.
Теоретична механіка розглядає кутову швидкість і кутове прискорення не тільки як алгебраїчні параметри обертального руху, але і у вигляді векторних величин.
Вектором кутової швидкості 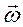 називають вектор, рівний за модулем алгебраїчній кутовій швидкості і напрямлений вздовж осі обертання тіла в той бік, звідкіля обертання тіла спостерігається як рух проти ходу годинникової стрілки.
називають вектор, рівний за модулем алгебраїчній кутовій швидкості і напрямлений вздовж осі обертання тіла в той бік, звідкіля обертання тіла спостерігається як рух проти ходу годинникової стрілки.
Вектор 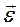 , рівний за модулем величині кутового прискорення і напрямлений вздовж осі обертання тіла в той бік, звідкіля бертання тіла спостерігається як рух проти ходу годинникової стрілки, називають вектором кутового прискорення.
, рівний за модулем величині кутового прискорення і напрямлений вздовж осі обертання тіла в той бік, звідкіля бертання тіла спостерігається як рух проти ходу годинникової стрілки, називають вектором кутового прискорення.
При цьому
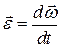 . .
| (23.6) |
Вектори 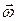 і
і  , для яких суттєве значення мають лише модулі і лінії дії, являють собою ковзні вектори.
, для яких суттєве значення мають лише модулі і лінії дії, являють собою ковзні вектори.
У випадках, коли 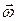 і
і  мають один напрям, тіло обертається прискорено; якщо
мають один напрям, тіло обертається прискорено; якщо 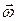 і
і  протилежних напрямів, то тіло обертається сповільнено (рис. 2.11).
протилежних напрямів, то тіло обертається сповільнено (рис. 2.11).
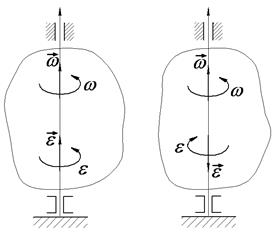
Рис. 23.5
Дата добавления: 2016-01-26; просмотров: 2156;
