Диференціальні рівняння рухів твердого тіла

Довільний рух твердого тіла можна розглядати як суперпозицію його поступального та обертального рухів. Взагалі говорячи, в механічній системі кожне з тіл може здійснювати вказані вище рухи. Обмежимося розглядом тих випадків, коли всі тіла системи здійснюють рух в одній площині (наприклад, ), який часто зустрічається на практиці. Тоді для поступального руху будемо мати рівняння

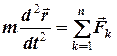, (4.1)

а для обертального руху навколо вісі, яка перпендикулярна до даної площини

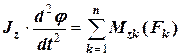. (4.2)

У випадку плоского руху, який можемо розглядати як суперпозицію поступального руху центру маси та обертального навколо центру маси, записуємо одразу два рівняння (4.1) – руху центру маси та (4.2) – обертання навколо центру маси.

У наведених рівняннях: 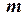- маса тіла, 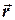- радіус-вектор його центра маси, 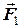, , 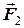..., - сили, що лежать у площині та діють на дане тіло, - його момент інерції відносно вісі обертання, 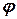- кут повороту тіла, - момент, який створює кожна з сил відносно вісі обертання.

Якщо тіло буде здійснювати плоскопаралельний рух, то отримуємо два рівняння (5.1 ) та (5.2), які описують поступальний рух центру маси тіла та його обертальний рух навколо цього центру.

Контрольні запитання

1. Запишіть диференціальне рівняння поступального руху твердого тіла. Поясніть величини, які входять у це рівняння.

2. Запишіть диференціальне рівняння обертального руху твердого тіла. Поясніть величини, які входять у це рівняння.

3. Запишіть диференціальні рівняння плоского руху твердого тіла. Поясніть величини, які входять у це рівняння.

Продемонструємо застосування наведених рівнянь при на конкретному прикладі. Механічна система (рис. 4.1) складається з бруска 1 ( 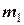= 5 кг), ступеневого блоку 2 ( 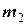= 4 кг, великий радіус 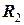= 20 см, малий 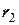= 10 см, 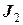= 0,2 кг×м²) та однорідного циліндра 3 ( 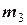= 22 кг, 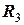= 10 см). Під дією сили тяжіння зі стану спокою тіла системи приходять у рух. Брусок 1 ковзає по похилій площині, яка утворює кут 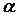= 30° до горизонту, коефіцієнт тертя ковзання 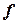= 0,2. Визначити прискорення тіл та натяги мотузок, якими з’єднані тіла механічної система. Тертя на осі блока 2 відсутнє, масою мотузок нехтувати, вважаючи їх нерозтяжними. Мотузка, що з’єднує тіло 1 та 2 паралельна похилій площині.

Розв’язання. Будемо вважати, що тіло 1 починає рух догори похилої площини і на момент, коли воно пройде шлях S₁, має прискорення .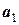

В цьому випадку тіло 2 буде обертатися за напрямом руху стрілки годинника з певним кутовим прискоренням 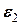, тіло 3 буде здійснювати плоскопаралельний рух, обертаючись проти напряму руху стрілки годинника з кутовим прискоренням 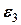, а його центр (вісь обертання блоку) буде рухатись вниз з лінійним прискоренням 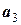(рис. 4.2).

З’ясуємо сили, які діють на кожне з тіл нашої системи щоб записати рівняння руху кожного тіла. Так, на перше тіло діють сила тяжіння 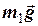, реакції опори 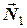, сили тертя 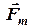та натягу мотузки 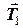. Векторна сума цих сил зумовлює прямолінійний рух першого тіла вздовж похилої площини

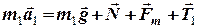. (1)

На друге тіло діють: сили тяжіння 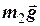, реакція осі блоку 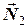та натяги мотузок 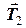та 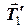. Сума моментів цих сил відносно нерухомої осі блоку 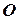зумовлює обертальний рух другого тіла. Оскільки моменти сил 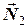та 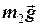відносно осі блоку дорівнюють нулю, рівняння обертального руху тіла 2 набуває вигляду

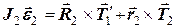, (2)

а відсутність поступального руху дає

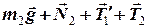= 0. (3)

На трете тіло діють сили натягу мотузок 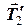, 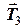та сила тяжіння 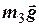- ці сили зумовлюють плоскопаралельний рух третього тіла, який запишемо як суперпозицію поступального руху його центра С з лінійним прискоренням та обертального руху навколо цього центру з кутовим прискоренням :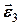

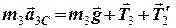, (4)

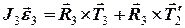. (5)

Послідовно отримаємо скалярні рівняння руху для кожного з тіл, які входять до нашої системи. Для першого тіла спрямуємо вісь 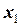декартової системи координат вздовж напряму його руху, вісь 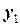перпендикулярно до похилої площини. В проекціях на обрані вісі отримуємо:

,

.

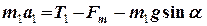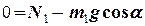З останнього рівняння знаходимо

,

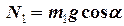що дає вираз для сили тертя

.

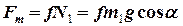Тоді для рівняння поступального руху тіла 1 отримуємо

. (6)

Для другого тіла введемо декартову систему координат 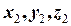. Спря-муємо вісі 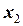та 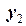горизонтально та вертикально і тоді в проекціях на ці вісі отримаємо

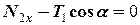, (7)

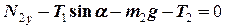. (8)

Вісь 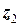спрямуємо через центр блоку перпендикулярно площині рисунку від нас і отримаємо рівняння його обертального руху

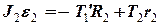. (9)

Рух третього тіла можна визначити як суперпозицію поступального руху його центра маси С з лінійним прискоренням 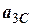та обертальним рухом навколо цього центру з кутовим прискоренням 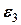. Для цього тіла, яке здійснює плоскопаралельний рух, вісь 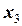спрямуємо вздовж прискорення поступального руху (вниз), а вісь обертання 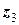– проведемо через його центр маси перпендикулярно до площини рисунку до нас (в напрямі кутового прискорення тіла). Тоді рівняння поступального руху центра третього тіла та обертального руху навколо його осі набувають вигляду:

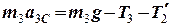, (10)

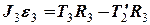, (11)

де 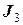- момент інерції циліндру відносно осі .

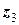Таким чином, ми отримали систему шести рівнянь (6) – (11) з одинадцятьма невідомими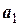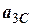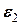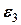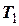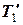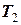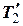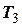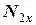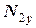: , , , , , , , , , , . Щоб система рівнянь стала повною, скористуємось третім законом Ньютона і умовою невагомості та нерозтяжності мотузок:

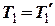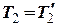, . (12)

Умови відсутності деформацій мотузок дає рівняння, які зв’язують між собою швидкості тіл системи. Швидкість точки А (дотику мотузки до зовнішньої поверхні блока 2) співпадає зі швидкістю першого тіла, тому

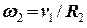. (13)

Трете тіло здійснює плоскопаралельний рух з ненульовою кутовою швидкістю 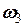, отож, це тіло має миттєвий центр швидкостей (МЦШ) навколо якого воно здійснює обертальний рух. МЦШ розташований в точці Р – дотику циліндра до нерухомої мотузки. Рівність лінійних швидкостей точок ( ) та D ( 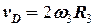) дає зв’язок між кутовими швидкостями блоку 2 та циліндра 3

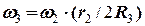. (14)

Лінійна швидкість центру циліндра зв’язана з його кутовою швидкістю

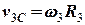. (15)

Шляхом диференціювання обох частин рівнянь (13), (14) та (15) отримуємо:

, (16)

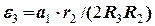, (17)

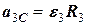. (18)

З (18) знаходимо зв’язок лінійного прискорення точки С з лінійним прискоренням першого тіла

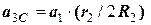. (19)

Система рівнянь (6)–(11) розпадається на дві незалежні: (6,9 – 11) та (7 –8). Підставимо отримані співвідношення (12) та (16-18) та в систему рівнянь (6,9 – 11):

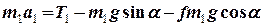, (20)

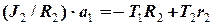, (21)

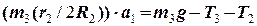, (22)

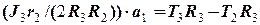. (23)

Розв’язок системи чотирьох рівнянь з чотирма невідомими 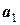, , 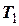, 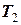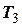є суто алгебраїчною задачею, яка може буди розв’язана різними методами

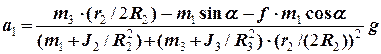. (24)

Для проведення розрахунків, візьмемо до уваги, що момент інерції однорідного циліндра визначається за формулою 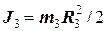= 0,025 кг^.∙м². Підставляючи дані задачі, отримуємо

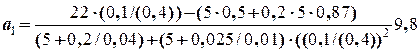= 2,12 (м/с²),

що дозволяє отримати вирази для натягу ниток 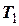, , 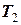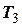з рівнянь (20) – (22).

Остійність судна

Умова плавання судна тіл зводиться до рівності його ваги 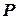та сили Архімеда. Оскільки вага судна

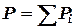, (5.1)

де сума береться по всім частинам самого судна та по всім вантажам та запасам на судні. Центр ваги знаходиться в точці 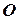, координати якої:

,

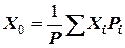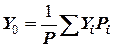, (2.2)

.

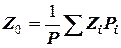Зауважимо, що в більшості посібників по теорії суден положення центру ваги позначають літерою .

Для розрахунку центру ваги судна складають таблиці, куди заносять всі елементи порожнього судна і доповнюють її даними по його запасах та вантажах, які перевозять.

Зауважимо, що завантаження потрібно проводити так, щоб був незначний нахил на корму (диферент 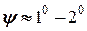) для збільшення сили тяги (рис. 5.1) та щоб не виникало бортового крену ( рис. 5.2).

Сила Архімеда виникає за рахунок тиску води на усю підводну поверхню судна. На кожний елемент поверхні 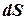діє сила 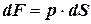(тут 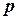- тиск рідини на площадку), яка направлена перпендикулярно поверхні. Рівнодійна всіх цих сил, що діють на підводну частину судна, дає силу Архімеда, яка направлена вертикально вверх і дорівнює:

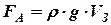, (2.3)

де 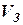- об’єм зануреної частини судна, 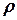- густина води, відповідно. Тобто сила Архімеда визначається вагою рідини, яку витісняє судно, тому в суднобудуванні її називають водотоннажністю. Точка прикладання цієї сили співпадає з центром витісненої рідини і називається центром величини. Зауважимо, що центр ваги судна лежить вище центра величини (рис.5.2).

Плавучість – це здатність судна тримати вертикальну рівновагу. Тоді умова плавучості судна має вид:

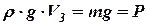, (2.4)

звідки знаходимо

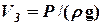. (2.5)

Крім того, для рівноваги двох сил 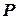та 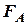необхідно, щоб вони не створювали моменту, тобто діяли по одній прямій в різні боки. Тобто центр ваги 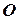та центр величини зануреного об’єму мають лежати на одній вертикалі. Тоді вертикальна лінія, що проходить через точки 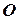та має бути перпендикулярною до площини ватерлінії ВЛ.

Оскільки при нахилах судна його вага не змінюється, то не змінюється як його положення центра ваги, так і загальний об’єм підводної частини судна. Отже, судно здійснює рівнооб’ємні нахили. Тому величина і напрямок сили 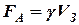не змінюється, але центр величини переміщується в той бік, куди нахиляється судно по дузі 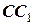. Центр кривизни лінії (точка на рис.5.1), по якій переміщується центр величини в результаті нахилу судна, називається метацентром, а радіус її кривизни 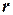– метацентричним радіусом. Таким чином метацентр - це точка перетину лінії дії сил плавучості при безмежно малому рівнооб’ємному нахилі судна в заданій площині з лінією 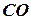, а метацентричний радіус – це висота метацентра над центром величини.

Оскільки судно можна нахиляти як в поперечній, так і в продольній площинах (рис.5.1 та 5.2), тому існує 2 метацентричних радіуса: поперечний 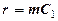(рис.5.1), який використовують при розрахунках поперечної остійності судна, та поздовжній 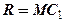(рис. 5.2), який використовують при розрахунках поздовжньої остійності судна.

Статична остійність судна. В результаті нахилу судна виникає момент сили тяжіння та виштовхувальної сили. Положення рівноваги може бути стійким або нестійким. Статична стійкість судна називається остійністю - це здатність судна повертатися до положення рівноваги за рахунок внутрішніх сил, коли судно вивели з положення рівноваги, але призупинили дію зовнішньої сили. Судно вважається остійним, якщо його рівновага стійка та не остійним, коли його рівновага нестійка. Мірою остійності судна є метацентрична висота (рис.5.1):

(2.6)

– висота метацентра над центром ваги.

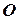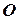Щоб положення судна було стійким, або як кажуть, судно зберігало остійність, необхідно, щоб точка перетину лінії по якій діє виштовхувальна сила при нахилі корабля з площиною його симетрії, тобто точка , лежала вище центра тяжіння тіла (рис.5.3). Дійсно, при малих кутах нахилу, якщо метацентр вище центра ваги , тобто 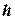>0, тоді сили ваги та сили плавучості створюють відновлюючий момент:

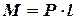, (2.7)

де 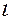- перпендикуляр, опущений з центру ваги на лінію дії сили Архімеда, який називається плечем статичної остійності. Враховуючи відхилення на малі кути, маємо:

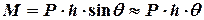, (2.8)

який намагається повернути судно в положення рівноваги.

У випадку 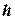=0 та 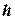<0 рівновага судна нестійка (рис.5.4). Отже метацентр – це висота, до якої можна піднімати центр ваги судна, залишаючи його рівновагу стійкою. Для більшості суден дотримуються того, щоб при повному навантаженні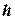 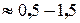м.

Щоб визначити остійність судна, до нього прикладають сталий момент сил , що викликає його нахил на кут 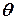. Для створення моменту використовують крен-баласти, а визначають нахил судна за допомогою інклінографа. Тоді з умови рівноваги судна (2.8) отримуємо вираз для метацентричної висоти:

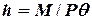. (2.9)

Судну придають таку форму, щоб положення метацентра при відхиленні на малі кути практично не змінювались при нахилі судна, одначе, при великих кутах нахилу судна метацентр може стати нижче центра тяжіння і тоді судно перекинеться.

При нахилі судна на великий кут розглянемо лише крен, бо великого диференту практично не виникає. В цьому випадку сили 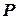та 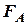створюють пару сил, відновлюючий момент якої:

= , (2.10)

де плече статичної остійності 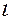залежить від форми підводного об’єму судна та від кута нахилу 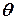, що зображено на рис.5.5.

По цій діаграмі (статичної остійності судна) для кожного кута нахилу знаходимо момент сил, який намагається повернути судно в положення рівноваги. Небезпечно нахиляти судно на кути 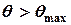, бо тоді величина моменту зменшується. Діаграма статичної остійності судна симетрична відносно від’ємних значень кута 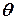(тобто нахилу на лівий борт).

Найбільшому значенню ординати відповідає найбільше значення плеча 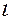і відновлюючого моменту, а кут нахилу 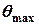, при якому досягаються ці значення – кутом максимуму діаграми остійності при якому судно буде в положенні стійкої рівноваги. При нахилі на кути більші 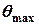зменшується значення плеча 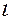та відновлюючого моменту і досягається такий кут 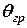, коли 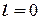(тоді 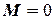). Абсциса цієї точки дорівнює граничному куту, якому відповідає положення нестійкої рівноваги, бо при нахилі на ще більший кут 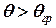судно перекинеться.

Динамічною остійністю називається здатність судна витримувати, не перекидаючись динамічну дію пари сил, що його нахиляє. В задачі про статичну рівновагу вважалось, що момент сил, які викликають нахил тіла прикладаються безмежно довго, так що в кожний момент часу рівновага встигає встановитись. Тепер нас буде цікавити динаміка процесу, коли момент, що викликає нахил досягає свого значення за дуже короткий момент часу (значно менший за період коливання судна), тобто практично миттєво. Така ситуація виникає, коли на судно раптово налітає хвиля або порив вітру (шквал). Тоді судно дістає динамічний нахил (крен).

Для спрощення задачі будемо вважати, що момент сили 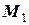, що викликає нахил судна, не залежить від кута нахилу 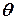. В цьому випадку на діаграмі статичної остійності (рис.5.6) будемо мати пряму лінію 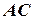, паралельну осі 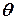. Цьому моменту відповідає статичний нахил судна 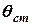. Однак при нахилі судна від 0 до 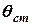момент 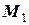більший від моменту, який відновлює рівновагу 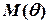. Тому 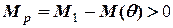і тоді в цій області:

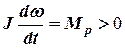, (4.1)

отже кутова швидкість судна зростає і в точці 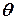= 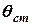досягає максимального значення. При 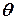> 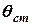, результуючий момент 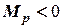, кутове прискорення стає від’ємним і кутова швидкість зменшується, але нахил корабля продовжує збільшуватись. Так буде відбуватись до тих пір поки кутова швидкість не стане рівною нулю. При цьому судно дістає нахил 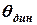, який знайдемо з умови рівності робіт моменту сили, який нахиляє судно та моменту сил остійності форми , що відновлюють положення судна:

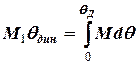. (4.2)

Найпростіше знайти розв’язок цього рівняння графічно. Оскільки фізичний зміст інтеграла, це площа під кривою, то треба знайти таке значення 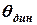_, щоб площі, які відповідають праві та лівій частині рівняння (4.2) були одинакові, тобто

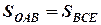. (4.3)

Графічний метод легко дозволяє визначити критичне значення моменту 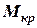, що нахиляє судно, при якому ще можливе повернення судна до положення рівноваги. Цьому випадку відповідає найбільше можливе значення рівності площ

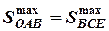, (4.4)

що зображено на рис.5.6. Звідки визначаємо критичний динамічний кут нахилу судна 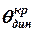_. Зауважимо, що він менший ніж критичний статичний кут нахилу , тобто:

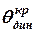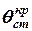< . (4.5)

Якщо > 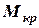_., то при динамічній його дії судно перекинеться. А якщо ≤ 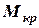, то судно нахилиться на певний кут, який виведемо з рівняння (4.2), а потім нахил буде зменшуватись, судно пройде положення рівноваги і нахилиться на протилежний бік, здійснюючи коливання. За рахунок сил тертя ці коливання будуть загасаючі. Амплітуда коливань буде зменшуватись поки не досягне статичної рівноваги, якій відповідає кут нахилу 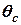при умові, що момент сил, який викликає нахил судна продовжує діяти (наприклад, швидкість вітру протягом певного часу не змінилась).

§ 6. Бортові та кільові коливання судна,