Розглядаємо абсолютний рух суден
 Спочатку розв’яжемо задачу, розглядаючи рух кожного судна відносно води. В абсолютній (нерухомій відносно поверхні Землі) ситемі відліку введемо декартову систему координат. ЇЇ початок сумістимо з судном
Спочатку розв’яжемо задачу, розглядаючи рух кожного судна відносно води. В абсолютній (нерухомій відносно поверхні Землі) ситемі відліку введемо декартову систему координат. ЇЇ початок сумістимо з судном  (рис.2.1) та направимо вісь
(рис.2.1) та направимо вісь 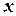 горизонтально, а вісь
горизонтально, а вісь 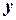 по норду (
по норду ( 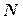 ).
).
Перш за все графічно визначимо схему розходження суден. По заданому пеленгу  з точки
з точки  проводимо промінь та у вибраному масштабі (наприклад, 1 см = 1 миля) відкладаємо на ній величину
проводимо промінь та у вибраному масштабі (наприклад, 1 см = 1 миля) відкладаємо на ній величину  і знаходимо початкове положення судна
і знаходимо початкове положення судна  (рис.1). З точок
(рис.1). З точок  і
і  по заданим курсам
по заданим курсам  та
та  (відкладених від норду
(відкладених від норду 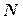 за стрілкою годинника) проводимо промені та отримуємо траєкторії абсолютного руху суден. Оскільки траєкторії перетинаються, то потрібно розв’язувати задачу на розходження.
за стрілкою годинника) проводимо промені та отримуємо траєкторії абсолютного руху суден. Оскільки траєкторії перетинаються, то потрібно розв’язувати задачу на розходження.
За відомими значеннями швидкості, визначаємо шлях, яке проходить кожне судно за  = 6 хв. = 0.1 год
= 6 хв. = 0.1 год  = 12 хв. = 0.2 год. та
= 12 хв. = 0.2 год. та  = 18 хв. = 0.3 год. і на траєкторіях абсолютного руху суден
= 18 хв. = 0.3 год. і на траєкторіях абсолютного руху суден  та
та  позначаємо відповідні положення суден через проміжки часу
позначаємо відповідні положення суден через проміжки часу  ,
,  та
та  (рис.1). Вимірюємо відстані між суднами та пеленги судна
(рис.1). Вимірюємо відстані між суднами та пеленги судна  у ці моменти часу і отримуємо:
у ці моменти часу і отримуємо: 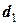 = 7,5 милі,
= 7,5 милі,  = 5,8 милі та
= 5,8 милі та 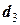 = 3,9 милі.
= 3,9 милі.  = 590 ,
= 590 ,  = 540 та
= 540 та  = 440. Оскільки пеленг судна
= 440. Оскільки пеленг судна  зменшується
зменшується  <
< 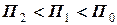 , то в даній задачі судно
, то в даній задачі судно  проходить перед судном
проходить перед судном  (по носу судна
(по носу судна  ). Якби зміна пеленгу була зворотною, то судно
). Якби зміна пеленгу була зворотною, то судно  проходило би перед судном
проходило би перед судном  (по носу судна
(по носу судна  ).
).
Для визначення найкоротшої відстані при розходженні та моменту, коли воно відбудеться, розв’яжемо задачу, розглядаючи абсолютний рух кожного судна. Для введеної системи координат початкові умови (при  ) дають:
) дають:
 ,
,
 (в милях),
(в милях),
а рівняння абсолютного руху кожного судна має вигляд
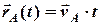 , (2.1)
, (2.1)
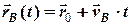 (2.2)
(2.2)
де вектори 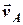 ,
, 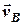 та
та 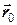 задані своїми напрямами та чисельними значеннями.
задані своїми напрямами та чисельними значеннями.
З рівнянь (2.1) та (2.2) визначаємо координати суден  та
та  у заданий момент часу
у заданий момент часу  :
:
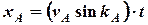 , (2.3)
, (2.3)
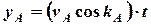 , (2.4)
, (2.4)
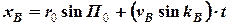 (2.5)
(2.5)
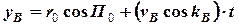 (2.6)
(2.6)
(всі віддалі в милях, а швидкості у вузлах 1вузол = 1миля/год  0,514м/с).
0,514м/с).
З системи рівнянь (2.3) – (2.6) розраховуємо у довільний момент часу  відстань
відстань  між судном
між судном  та
та  і пеленг
і пеленг 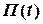 судна
судна  за формулами:
за формулами:
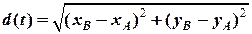 =
= 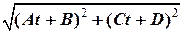 , (2.7)
, (2.7)
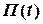 =
=  , (2.8)
, (2.8)
де
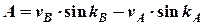 = - 18,69 (вуз.), (2.9)
= - 18,69 (вуз.), (2.9)
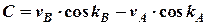 = - 5,22 (вуз.), (2.10)
= - 5,22 (вуз.), (2.10)
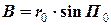 = 8,30 милі, (2.11)
= 8,30 милі, (2.11)
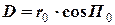 = 4,41 милі. (2.12)
= 4,41 милі. (2.12)
З отриманих формул у моменти часу  ,
, 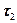 та
та  знаходимо:
знаходимо:
 = 0,49,
= 0,49,  = 1,52,
= 1,52, 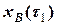 = 6,92,
= 6,92, 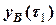 = 5,41,
= 5,41, 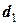 = 7,52,
= 7,52,  = 58,30;
= 58,30;
 = 0,99,
= 0,99, 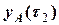 = 3,04,
= 3,04, 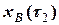 = 5,55,
= 5,55,  = 6,41,
= 6,41,  = 5,67,
= 5,67,  = 53,60.
= 53,60.
 = 1,48,
= 1,48, 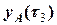 = 4,57,
= 4,57,  = 4,17,
= 4,17,  = 7,41,
= 7,41, 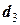 = 3,92,
= 3,92,  = 43,40,
= 43,40,
що співпадає з результатами, які ми отримали з рис.1
Використовуючи комп’ютерну графіку, розраховуємо відстань між  суднами і будуємо залежність
суднами і будуємо залежність  , яка зображена на рис.2.2. З графіка видно, що величина відстані
, яка зображена на рис.2.2. З графіка видно, що величина відстані  між суднами змінюється не монотонно. Мінімум кривої дозволяє визначити найменшу відстань між суднами
між суднами змінюється не монотонно. Мінімум кривої дозволяє визначити найменшу відстань між суднами 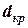
 2 милі та момент часу
2 милі та момент часу 
 0,47 год
0,47 год  28 хв., коли це відбудеться.
28 хв., коли це відбудеться.
Аналітично найменшу віддаль між судами 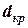 знаходимо з умови рівності нулю похідної:
знаходимо з умови рівності нулю похідної:  , що згідно рівнянню (7) дає:
, що згідно рівнянню (7) дає:
 . (2.11)
. (2.11)
Звідки визначаємо час  , коли судна розійдуться на найменшій відстані
, коли судна розійдуться на найменшій відстані
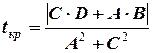 . (2.12)
. (2.12)
Для визначення 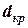 необхідно підставити значення
необхідно підставити значення  у вираз для
у вираз для  і тоді отримуємо:
і тоді отримуємо:
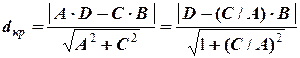 (2.13)
(2.13)
З врахуванням даних задачі, визначаємо:  = 0,45 год.
= 0,45 год.  27 хв.,
27 хв., 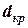 = 2,0 милі.
= 2,0 милі.
Дата добавления: 2015-12-10; просмотров: 686;
