Розглядаємо відносний руху суден
Аналіз розв’язку показує, що задача зводиться до визначення відносної віддалями між суднами, тобто визначальною є відносна швидкість суден. Тому розв’яжемо задачу, розглядаючи відносний рух суден.
Абсолютна швидкість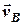 
будь-якої точки 
(відносно нерухомої системи відліку) при складному рухові визначається формулою
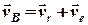, (2.14)
де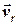 
– відносна швидкість точки в рухомій системі та 
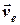– переносна швидкість точки за рухонок руху системи. Звідки для швидкості відносного руху точки отримуємо
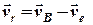. (2.15)
Введемо рухому систему відліку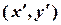 
, а її центр у початковий момент часу сумістимо з судном 
. У наступні моменти часу центр цієї системи 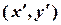буде рухатися зі швидкістю 
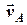по траєкторії 
(рис.2.1) абсолютного руху судна . При цьому декартові вісі абсолютної та рухомої систем будуть залишатися паралельними (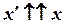 
та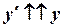 
). Тоді швидкість точки буде відігравати роль переносної швидкості
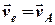. (2.16)
Отже, в системі 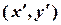судно буде залишатися нерухомим, а судно буде рухатися з відносною швидкістю 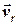, яку знаходимо з формули (2.15) з урахуванням (2.16)
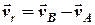. (2.17)
Спочатку розв’яжемо задачу графічно. За допомогою транспортира та лінійки будуємо початкове положення суден та . Оберемо зручний для швидкостей масштаб, наприклад, 1 см = 2 вузла та побудуємо вектори швидкостей суден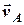 
та 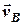(рис.3). Щоб графічно побудувати вектор відносної швидкості 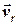треба до вектора 
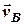додати вектор ( 
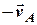) (рис. 2.3).
Траєкторія руху судна В відносно нерухомого судна А лежить на векторі 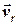і визначає лінію 
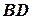відносного руху. Положення цієї лінії свідчить про те, що в нашому випадку судно В пройде перед судном судна А (по носу).
Для того, щоб знайти найкоротшу відстань між суднами, треба з точки А опустити перпендикуляр на лінію відносного руху 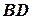– так ми отримуємо точку С. Вимірюємо мінімальну відстань між суднами dкр = 
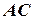= 2,1 милі.
Щоб визначити час розходження, потрібно відстань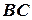 
(вимірювання дає 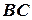≈ 9,1 миль) поділити на швидкість відносного руху. Вимірюємо довжину вектора 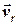та знаходимо модуль відносної швидкості 
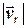= 19,5 вузлів. Отже 
= 9,1/19,5 ≈ 0,47 годин 
28 хв.
Щоб розв’язати задачу аналітично,запишемо вирази для векторів швидкостей суден. Оскільки декартові вісі рухомої та абсолютної систем лишаються паралельними, то:
= 
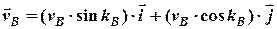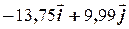, (2.18)
= 
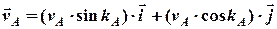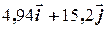. (2.19)
Тоді для вектора відносної швидкості отримуємо
+ 
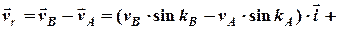
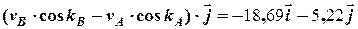(2.20)
Зауважимо, що отримані раніше вирази (2.9) та (2.10) для величин та визначають компоненти відносної швидкості. Після цього підрахуємо модуль відносної швидкості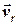
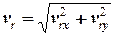= 19,4 (вуз.). (2.19)
Рівняння лінії відносного руху можна записати як рівняння прямої, що проходить через точку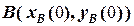 
вздовж вектора 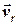, тому воно має вигляд
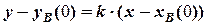, (2.20)
де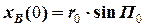 
= 8,30 (милі) та 
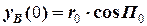= 4,41 (милі) та 
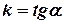– тангенс кута нахилу лінії відносного руху до осі x, який знаходимо через компоненти вектора відносного руху
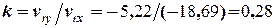. (2.21)
Найкоротша відстань між суднами визначиться віддаллю точки А(0,0) від цієї прямої, тому
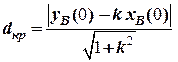. (2.22)
Зауважимо, що формула (22) співпадає з формулою (13). Підставляючи дані, отримуємо
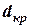= 2,00 (милі).
Для знаходження моменту часу, коли судно буде в точці 
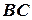, потрібно віддаль поділити на модуль відносної швидкості
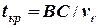. (2.23)
Величину 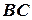розраховуємо їз прямокутного трикутника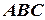 
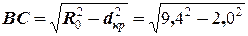= 9,18 (милі),
тоді
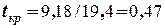(годин) » 28 (хв.)
Таким чином усіма методами отримали близькі результати, які вказують, що швидкість відносного зближення суден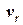 
= 19,4 вузла, вони розійдуться через 
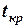» 28 хв. на найкоротшій відстані 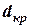= 2,0 милі.
Зауважимо, що підхід, коли задача зведена до їх відносного руху дозволяє узагальнити задачу на випадок руху суден в області дії постійної течії, бо відносна швидкість в цьому випадку не зміниться, дійсно
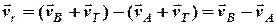. (2.24)
Дата добавления: 2015-12-10; просмотров: 599;