Вращение твердого тела вокруг неподвижной оси

Если во все время движения твердого тела две какие-либо его точки остаются неподвижными, то такое движение тела называется вращением вокруг неподвижной оси, а прямая, проходящая через две неподвижные точки, называется осью вращения тела.

При таком движении тела все его точки, не лежащие на оси вращения, будут описывать окружности с центром на оси вращения и с плоскостями, перпендикулярными ей.

Выберем неподвижную систему координат Оxyz, ось Oz которой совпадает с осью вращения твердого тела. Возьмем также систему Оx'y'z', вращающуюся вместе с телом. Положение подвижной системы относительно неподвижной будет определяться двугранным углом между плоскостями с xOz и x'Oz'. Обозначим его j. Угол j изменяется с течением времени и представляет собой некоторую непрерывную функцию времени t. Таким образом, закон вращательного движения твердого тела имеет вид:

.

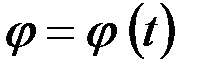За положительное направление j примем направление против часовой стрелки, если смотреть со стороны положительного направления оси Oz.

Угловая скорость

Для характеристики быстроты изменения j введем понятие угловой скорости.

Пусть в момент времени t положение тела определялось углом j (t), а в момент 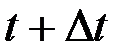углом j 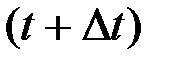. Тогда за время угол поворота получит приращение 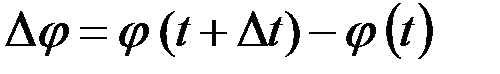. Отношение приращения 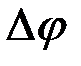к называется средней угловой скоростью тела за время :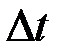

.

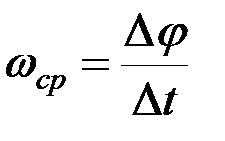Переходя к пределу при 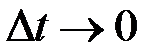, получим:

,

где – угловая скорость тела в данный момент времени.

Величина угловой скорости твердого тела при вращении его вокруг неподвижной оси равна первой производной от угла поворота по времени.

Знак w определяет направление вращения тела. Если вращение происходит против хода часовой стрелки, то w > 0, т.е. положительное приращение угла отсчитывается против хода часовой стрелки. Размерность угловой скорости – 1/c или .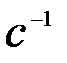

Угловую скорость можно изображать в виде вектора 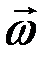, модуль которого равен 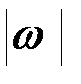и который направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки.

Угловое ускорение

Угловое ускорение характеризует изменение угловой скорости с изменением времени.

Если за промежуток времени 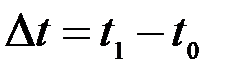угловая скорость изменится на величину 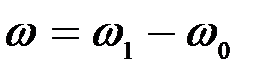, то числовое значение среднего углового ускорения равно:

.

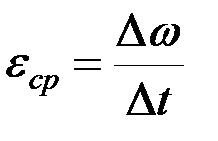Переходя к пределу при 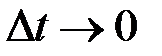, получим:

.

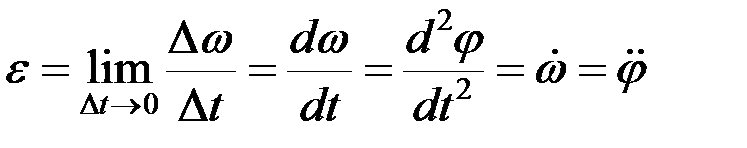Числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота по времени. Размерность углового ускорения – 1/c² или c ^–2.

Вектор углового ускорения направлен вдоль оси вращения: если 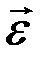совпадает с направлением , то вращение ускоренное, если нет – замедленное.