Естественный способ задания движения точки. Понятие о естественном трехграннике
 Построим к кривой АВ в точке M касательную, единичный вектор которой обозначим через
Построим к кривой АВ в точке M касательную, единичный вектор которой обозначим через 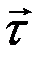 . Перпендикуляр к касательной называется нормалью. Очевидно, их может быть бесконечно большое
. Перпендикуляр к касательной называется нормалью. Очевидно, их может быть бесконечно большое  число. Все они будут лежать в плоскости, проходящей через точку M, и будут перпендикулярны касательной. Это нормальная плоскость к кривой в данной точке. Нормаль, лежащая в соприкасающейся плоскости (плоскости кривой), называется главной нормалью, ее единичный вектор
число. Все они будут лежать в плоскости, проходящей через точку M, и будут перпендикулярны касательной. Это нормальная плоскость к кривой в данной точке. Нормаль, лежащая в соприкасающейся плоскости (плоскости кривой), называется главной нормалью, ее единичный вектор 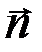 направлен в сторону вогнутости кривой АВ. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью, ее единичный вектор обозначим как
направлен в сторону вогнутости кривой АВ. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью, ее единичный вектор обозначим как 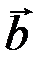 . Плоскость tМb называется спрямляющей плоскостью. Три взаимно перпендикулярные оси, имеющие начало в точке M и направленные по векторам
. Плоскость tМb называется спрямляющей плоскостью. Три взаимно перпендикулярные оси, имеющие начало в точке M и направленные по векторам 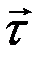 ,
, 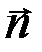 ,
, 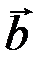 называются естественными или натуральными осями координат (оси естественного трехгранника). Такая система будет подвижной, так как при движении точки M начало координат и направление осей изменяется.
называются естественными или натуральными осями координат (оси естественного трехгранника). Такая система будет подвижной, так как при движении точки M начало координат и направление осей изменяется.
Пусть точка M движется по некоторой траектории 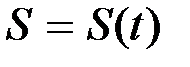 , лежащей в соприкасающейся плоскости. Найдем проекции ускорения на нормаль и касательную к траектории. Обозначим:
, лежащей в соприкасающейся плоскости. Найдем проекции ускорения на нормаль и касательную к траектории. Обозначим: 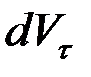 – проекция приращения вектора скорости на касательную, а
– проекция приращения вектора скорости на касательную, а 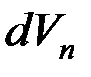 – проекция на нормаль. Пусть точка движется из положения M в положение M' и в этих точках имеет скорости
– проекция на нормаль. Пусть точка движется из положения M в положение M' и в этих точках имеет скорости 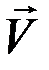 и
и 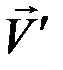 , тогда
, тогда 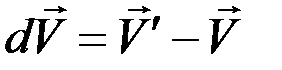 .
.
Тогда 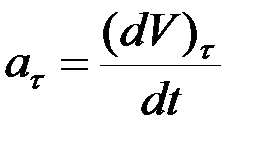 – касательное ускорение,
– касательное ускорение,
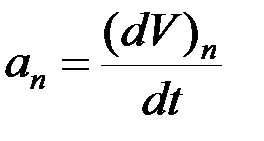 – нормальное ускорение.
– нормальное ускорение.
Перенесем вектор 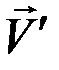 в точку M, при этом
в точку M, при этом 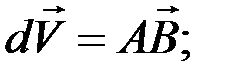
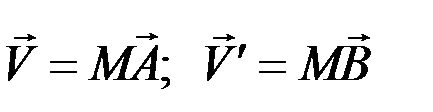 .
.
При 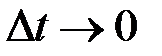
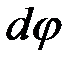 также стремится к нулю, а фигура АDBC стремится к прямоугольнику, в котором диагональ АВ стремится к АС. Так как
также стремится к нулю, а фигура АDBC стремится к прямоугольнику, в котором диагональ АВ стремится к АС. Так как 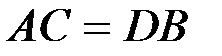 ,
, 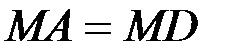 , то
, то 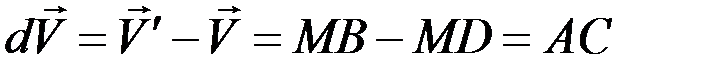 . Но АС – проекция
. Но АС – проекция 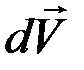 на касательную, то есть
на касательную, то есть 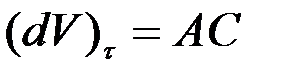 , тогда
, тогда 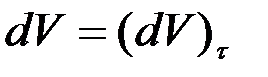 , следовательно,
, следовательно, 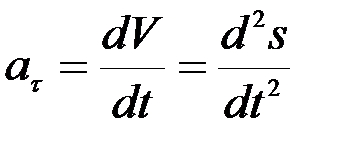 .
.
Далее, 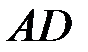 – это проекция
– это проекция 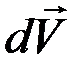 на нормаль, то есть
на нормаль, то есть 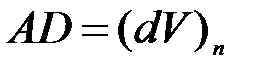 можно рассматривать как элементарную дугу радиуса MA, тогда
можно рассматривать как элементарную дугу радиуса MA, тогда 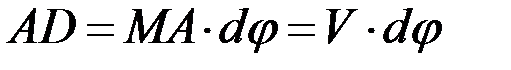 и, следовательно,
и, следовательно, 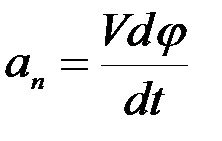 .
. 
Угол 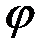 между касательной и кривой в двух ее точках называется углом смежности,
между касательной и кривой в двух ее точках называется углом смежности, 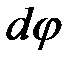 – элементарный угол смежности, тогда
– элементарный угол смежности, тогда 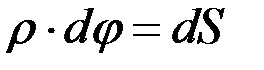 , где
, где 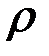 – радиус кривизны траектории, тогда
– радиус кривизны траектории, тогда
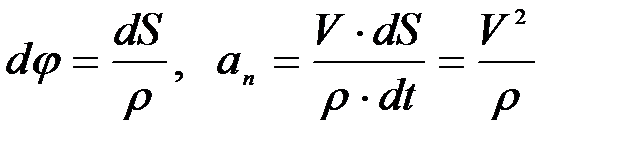 .
.
Тангенциальное (касательное) ускорение (проекция ускорения точки на касательную) равна первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) по времени. Нормальное (центростремительное) ускорение (проекция ускорения на главную нормаль) равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой.
Пусть точка M движется по кривой. Изобразим векторы 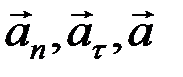 . Вектор нормального ускорения
. Вектор нормального ускорения 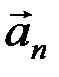 всегда направлен в сторону вогнутости кривой. Вектор
всегда направлен в сторону вогнутости кривой. Вектор 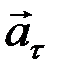 направлен по касательной к траектории как в сторону скорости (ускоренное движение), так и противоположно ей (замедленное движение).
направлен по касательной к траектории как в сторону скорости (ускоренное движение), так и противоположно ей (замедленное движение).
Полное ускорение точки:


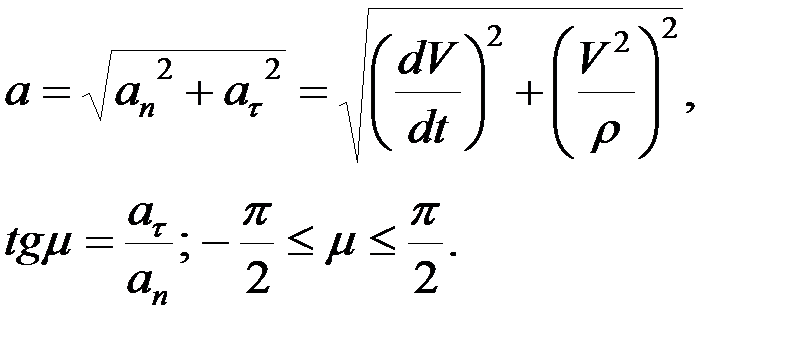
Дата добавления: 2015-12-26; просмотров: 1124;
