Естественный способ задания движения точки. При естественном способе задания движения задана траектория движения точки m в системе отсчета xyz

При естественном способе задания движения задана траектория движения точки m в системе отсчета xyz. Движение точки будет считаться заданным, если мы сможем в каждый момент времени указать ее положение на траектории.

Возьмем на траектории 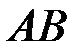точку и назовем ее началом отсчета. Измерим длину дуги 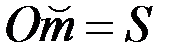(со знаком + или –). Длину дуги S называют дуговой координатой точки m. Заданием дуговой координаты 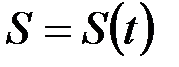для любого момента времени однозначно определяется положение точки на ее траектории. 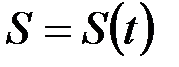– уравнение движения точки при естественном способе задания движения или закон движения точки.

Примечание: не следует путать пройденный путь и дуговую координату, так как в общем случае это не одно и то же. Путь всегда положителен, а координата нет. При движении по замкнутой траектории путь по модулю не равен координате.

Определение скорости точки при различных способах задания движения

Под скоростью точки подразумевается быстрота изменения радиуса-вектора или дуговой координаты точки, определяющей ее положение.