Определение скоростей точек твердого тела
Пусть оси 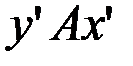 движутся вместе с точкой A, оставаясь параллельными осям xOy. Тогда положение точки M будет определяться радиус-вектором
движутся вместе с точкой A, оставаясь параллельными осям xOy. Тогда положение точки M будет определяться радиус-вектором 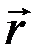 :
:
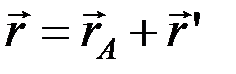 ,
,
где 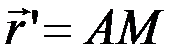 .
.
Тогда скорость точки определяется выражением
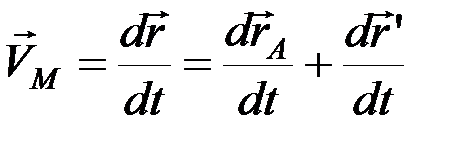 .
.
 В полученном равенстве
В полученном равенстве 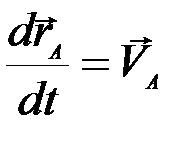 – скорость полюса A,
– скорость полюса A, 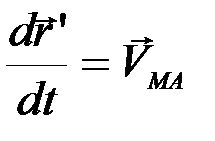 – скорость, которую точка M получает при
– скорость, которую точка M получает при 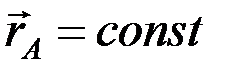 , то есть при вращении плоской фигуры относительно точки
, то есть при вращении плоской фигуры относительно точки 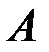 (полюса):
(полюса):
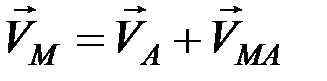 .
.
При этом 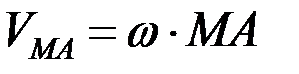
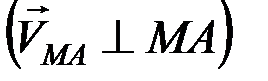 , где
, где  – угловая скорость фигуры.
– угловая скорость фигуры.
Теорема. Скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса.
Модуль и направление скорости 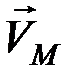 находятся путём построения параллелограмма.
находятся путём построения параллелограмма.
Теорема о проекциях скоростей двух точек тела
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу, то есть 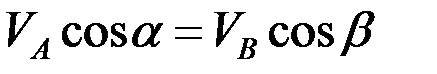 .
.
Доказательство.Разложим скорость 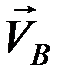 на две составляющие в соответствии с равенством
на две составляющие в соответствии с равенством 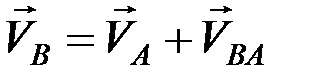 . Проецируя обе части равенства на ось, проходящую через точки
. Проецируя обе части равенства на ось, проходящую через точки 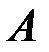 и
и 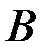 , получим
, получим
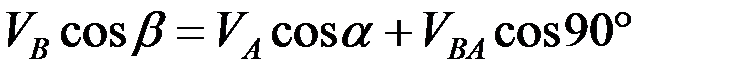 или
или 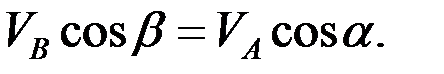
Дата добавления: 2015-12-26; просмотров: 929;
