Частные случаи определения мгновенного центра скоростей

 а) если движение осуществляется путем качения (без скольжения) одного цилиндрического тела по поверхности другого неподвижного тела, то точка Р катящегося тела, касающаяся неподвижного тела, имеет скорость
а) если движение осуществляется путем качения (без скольжения) одного цилиндрического тела по поверхности другого неподвижного тела, то точка Р катящегося тела, касающаяся неподвижного тела, имеет скорость 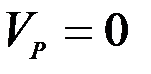 и, следовательно, является мгновенным центром скоростей;
и, следовательно, является мгновенным центром скоростей;
б) если скорости точек А и В параллельны друг другу, причем линия AB не перпендикулярна векторам скоростей, то мгновенный центр скоростей находится в бесконечности, а движение в данный момент времени поступательное;
в) если скорости точек А и В параллельны друг другу, и при этом АВ перпендикулярна векторам скоростей, то мгновенный центр скоростей Р определяется построением, показанным на рисунке;
г) если известны вектор скорости точки А и угловая скорость тела, то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к вектору скорости точки А, можно найти из равенства
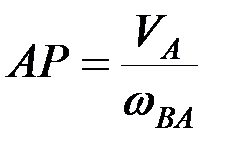 .
.
При движении плоской фигуры мгновенный центр скоростей непрерывно изменяет свое положение как на неподвижной плоскости, так и на подвижной, связанной с плоской фигурой. Геометрическое место мгновенного центра скоростей на неподвижной плоскости называют неподвижной центроидой, а на плоской фигуре – подвижной центроидой.
План скоростей
Планом скоростей называется диаграмма, на которой от некоторого центра отложены векторы скоростей точек тела.
Пусть 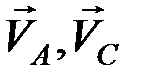 и
и 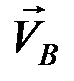 – скорости соответствующих точек тела. Отложим векторы скоростей, соответствующие в некотором масштабе отрезкам определенной длины, от произвольно выбранного центра О, тогда векторы
– скорости соответствующих точек тела. Отложим векторы скоростей, соответствующие в некотором масштабе отрезкам определенной длины, от произвольно выбранного центра О, тогда векторы 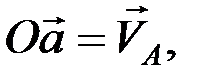
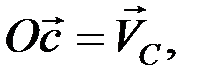
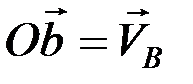 .
.
Допустим, что точка А – полюс, тогда 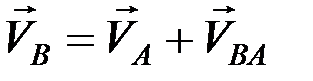 , где
, где 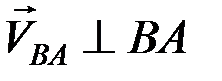 ,
, 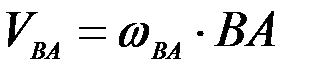 . Из диаграммы видно, что
. Из диаграммы видно, что 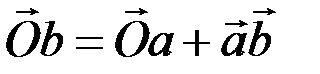 или
или 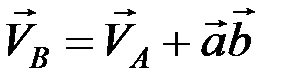 , следовательно,
, следовательно, 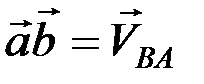 , тогда
, тогда 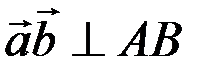 . Кроме того, так как
. Кроме того, так как 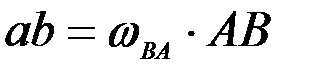 , то
, то 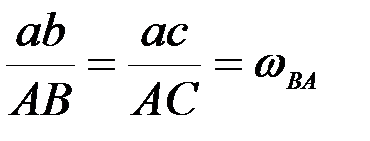 .
.
Отрезки, соединяющие концы векторов скоростей на плане скоростей, перпендикулярны отрезкам, соединяющим соответствующие точки тела, и по модулю пропорциональны этим отрезкам.
План скоростей позволяет получить скорость любой точки тела. План скоростей механизма строится как совокупность планов скоростей отдельных его звеньев (тел), причем все векторы скоростей откладываются от общего центра О, называемого полюсом плана скоростей.
Пример.Определить скорость ползуна В для показанного на рисунке положения механизма, если угловая скорость кривошипа ОА равна 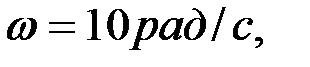
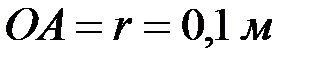 . Решение выполнить двумя способами:
. Решение выполнить двумя способами:
1) с использованием теоремы о проекциях скоростей двух точек тела;
2) построением мгновенного центра скоростей (МЦС) шатуна АВ.
Решение:
1. 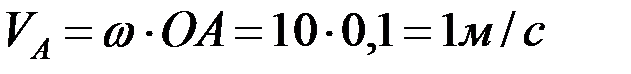 ,
, 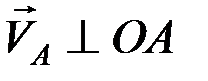 .
.
Т.к. скорость 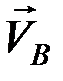 направлена вдоль оси ползуна, то, по теореме о проекциях скоростей, имеем:
направлена вдоль оси ползуна, то, по теореме о проекциях скоростей, имеем:
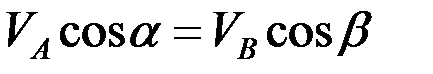
 ;
; 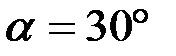 ;
; 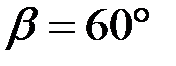 ;
;
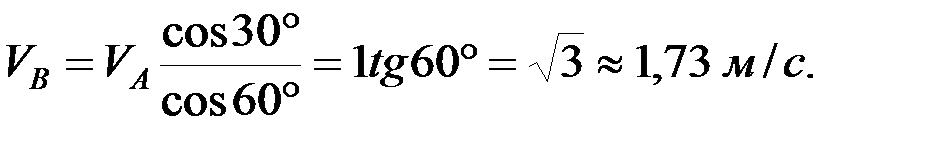
2. Найдем положение МЦС (точка Р, рис.), тогда
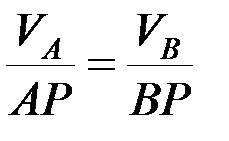 ,
, 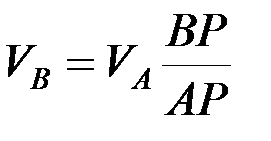 .
.
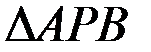 – прямоугольный, так как
– прямоугольный, так как 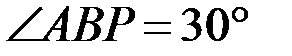 ;
; 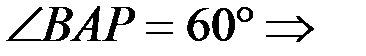
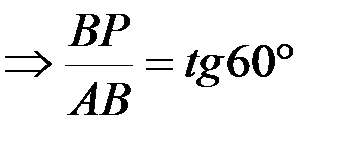 ,
, 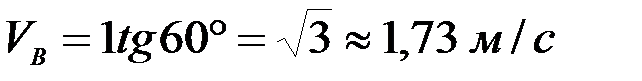 .
.
Лекция 7
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА (определение ускорений)
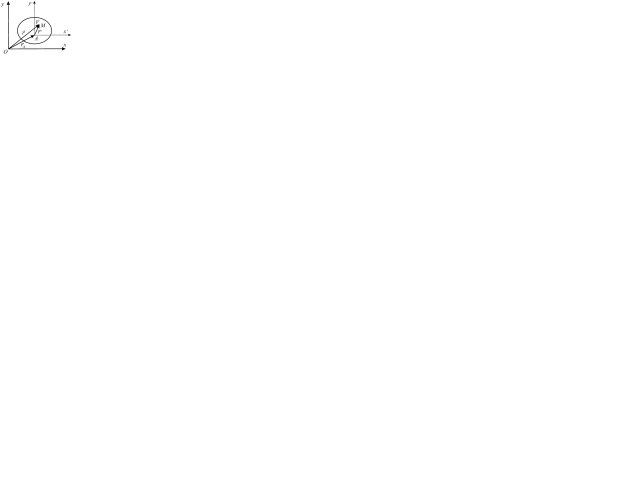 Пусть тело совершает плоское движение в координатах xOy. Требуется определить ускорение точки М. Обозначим полюс точкой А и проведем через него оси
Пусть тело совершает плоское движение в координатах xOy. Требуется определить ускорение точки М. Обозначим полюс точкой А и проведем через него оси 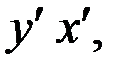 которые движутся вместе с полюсом А, оставаясь параллельными осям x и y. Обозначим положение точек А и М радиус-векторами:
которые движутся вместе с полюсом А, оставаясь параллельными осям x и y. Обозначим положение точек А и М радиус-векторами:
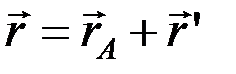 , где
, где 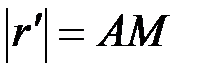 ,
,
тогда 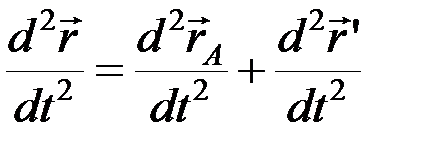 или
или 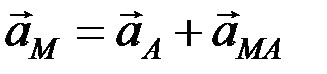 .
.
Так как 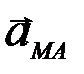 – ускорение во вращательном движении точки М вокруг точки А, то
– ускорение во вращательном движении точки М вокруг точки А, то 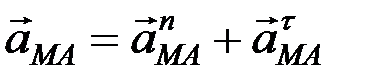 ,
,
где 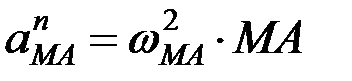 ,
, 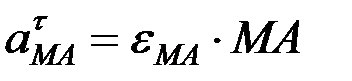 .
.
Таким образом, 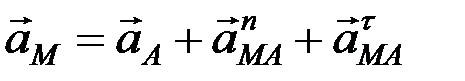 .
.
Ускорение любой точки 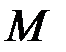 плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса.
плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса.
При этом вектор 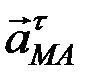 направлен перпендикулярно МА в сторону вращения, если движение ускоренное, и против вращения, если движение замедленное. Вектор
направлен перпендикулярно МА в сторону вращения, если движение ускоренное, и против вращения, если движение замедленное. Вектор 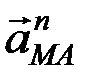 всегда направлен от точки М к точке А.
всегда направлен от точки М к точке А.
В общем случае, если движение полюса А является криволинейным, получим 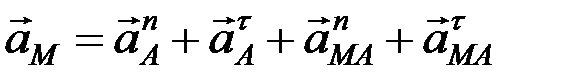 .
.
 Пример.Колесо катится без скольжения в вертикальной плоскости по наклонному прямолинейному пути. Найти ускорение концов двух взаимно перпендикулярных диаметров колеса, из которых один параллелен рельсу, если в рассматриваемый момент времени скорость центра колеса
Пример.Колесо катится без скольжения в вертикальной плоскости по наклонному прямолинейному пути. Найти ускорение концов двух взаимно перпендикулярных диаметров колеса, из которых один параллелен рельсу, если в рассматриваемый момент времени скорость центра колеса 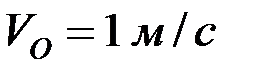 , ускорение центра колеса
, ускорение центра колеса 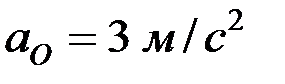 , радиус колеса
, радиус колеса 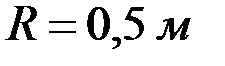 .
.
Решение.
Точка 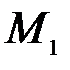 – мгновенный центр скоростей, следовательно, угловая скорость колеса равна:
– мгновенный центр скоростей, следовательно, угловая скорость колеса равна:
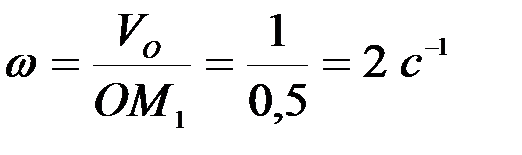 .
.
Угловое ускорение колеса равно:
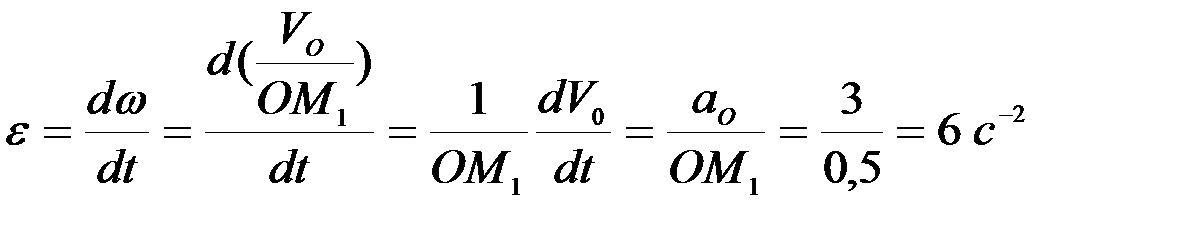 .
.
Примем за полюс точку О, тогда 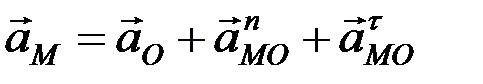 ,
,
где 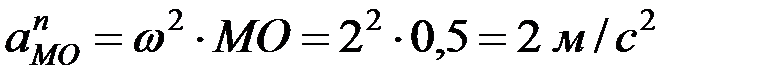 ,
, 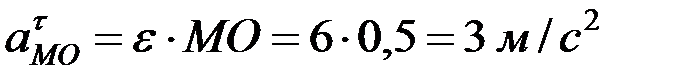 .
.
Решим задачу для точки 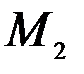 . Для этого покажем векторы ускорения.
. Для этого покажем векторы ускорения.
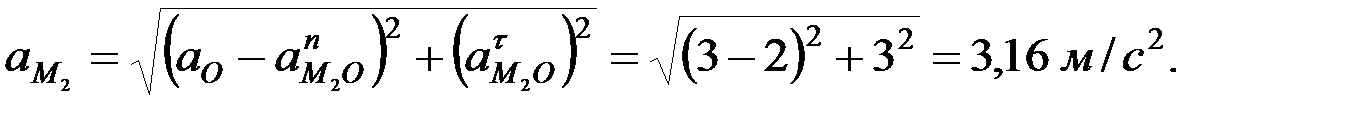
Решим задачу для точки 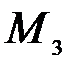 .
.

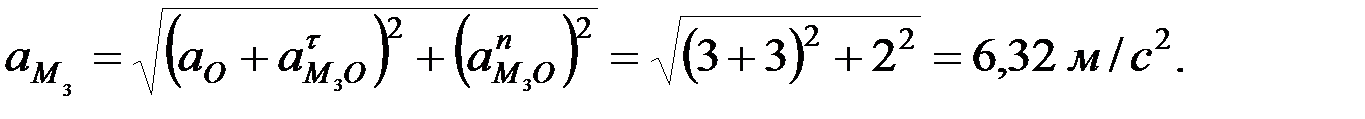
Решим задачу для точки  .
.

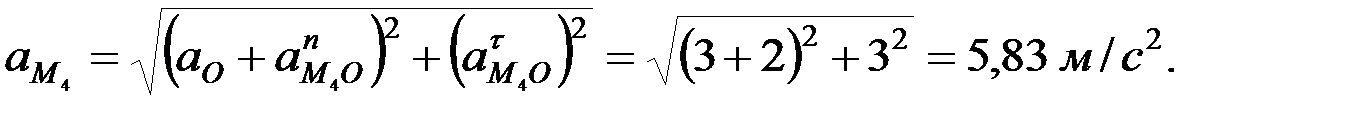
Решим задачу для точки  .
.
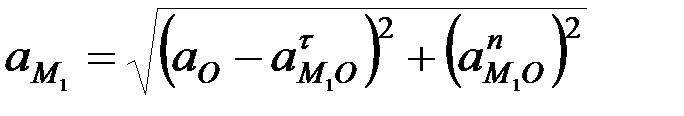
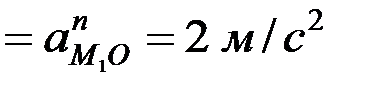 .
.
Пример.В механизме эллипсографа в данный момент времени ползун движется со скоростью 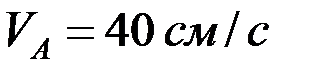 и ускорением
и ускорением 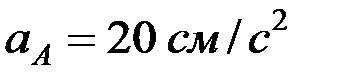 . Направления векторов указаны на рисунке. Длина стержня
. Направления векторов указаны на рисунке. Длина стержня 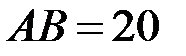 см. Определить скорость и ускорение ползуна В и точки С, лежащей в центре стержня АВ.
см. Определить скорость и ускорение ползуна В и точки С, лежащей в центре стержня АВ.
Решение:
1. Определим скорости точек В и C.
Скорость точки B направлена вниз вдоль направляющих. Определяем точку P – мгновенный центр скоростей:
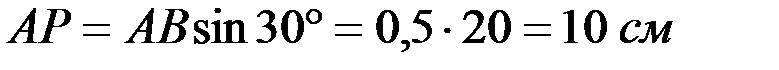 ,
,
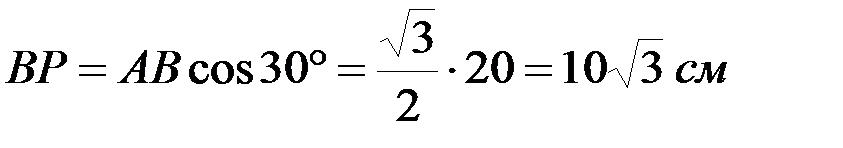 .
.
Так как 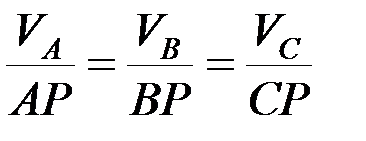 , то
, то 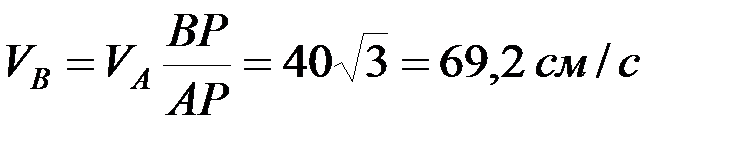 .
.
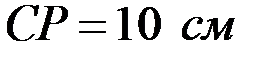 (как часть диагонали прямоугольника), поэтому
(как часть диагонали прямоугольника), поэтому



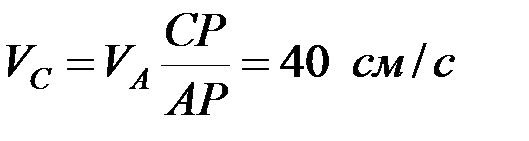 .
.
2. Определим ускорения точек В и C.
По теореме об ускорениях точек твердого тела при его плоском движении
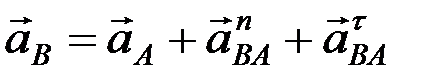 , (1)
, (1)
где 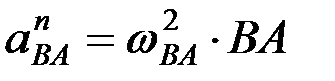 ,
, 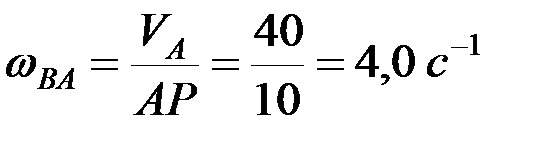 .
.
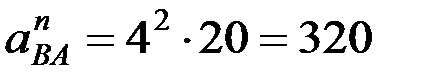
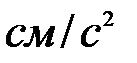 .
.
Величины 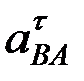 и
и 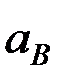 находим, проецируя равенство (1) на оси x и y:
находим, проецируя равенство (1) на оси x и y:
x: 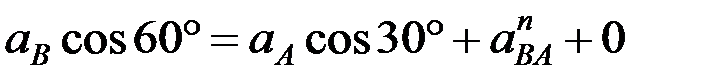 ,
,
y: 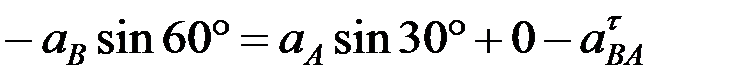 .
.
Откуда 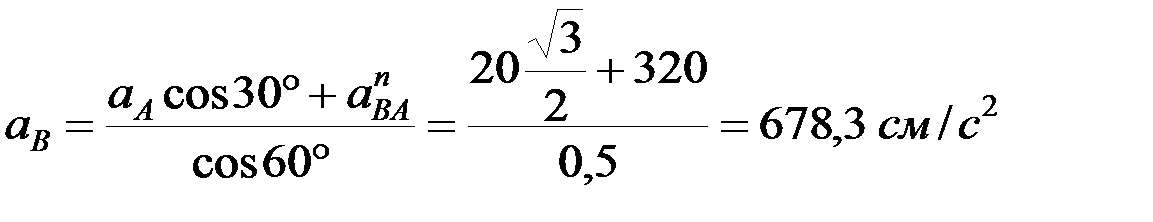 ,
,
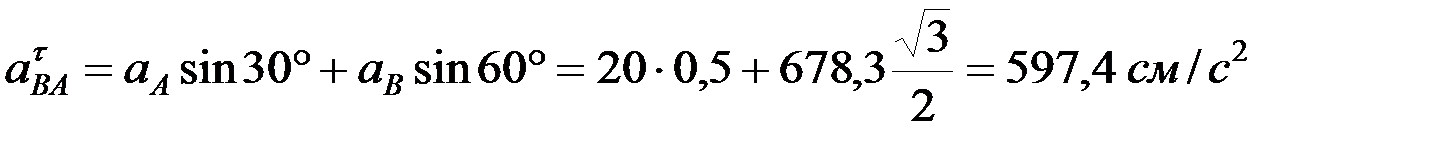 .
.
Т.к. 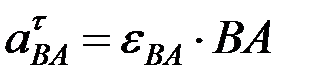 ,
,
то 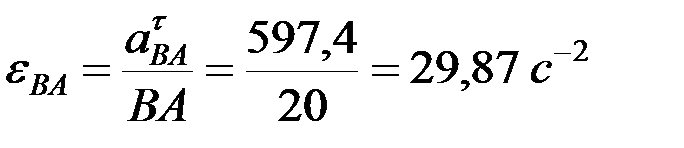 и направлено против часовой стрелки.
и направлено против часовой стрелки.
Для точки С имеем:
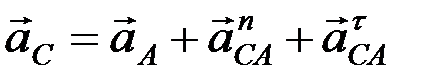 , (2)
, (2)
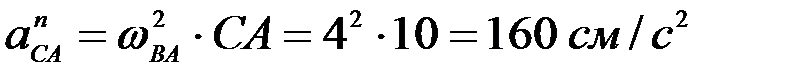 ,
,
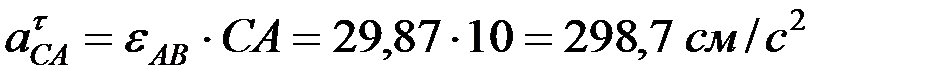 .
.
Проецируя выражение (2) на оси x и y, получим:
x: 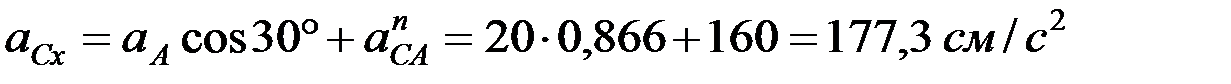 ,
,
y: 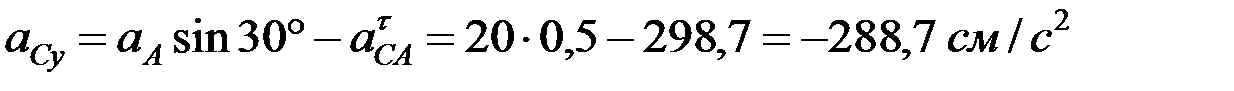 ;
;
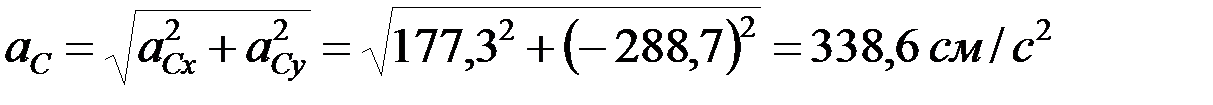 .
.
Дата добавления: 2015-12-26; просмотров: 1127;
