Розподіл швидкостей і прискорень точок тіла при обертальному русі
При обертанні твердого тіла навколо нерухомої осі будь-яка його точка (наприклад, точка М), що відстоїть від осі обертання на відстані 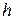 , описує коло радіуса
, описує коло радіуса 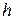 (рис. 23.4). Тоді, якщо за час
(рис. 23.4). Тоді, якщо за час 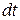 тіло обернеться на кут
тіло обернеться на кут 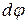 , точка
, точка  здійснить переміщення
здійснить переміщення 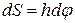 . Алгебраїчна швидкість точки на цьому переміщенні згідно з формулою (21.13)
. Алгебраїчна швидкість точки на цьому переміщенні згідно з формулою (21.13)
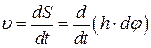 ,
,
або
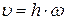 . .
| (23.7) |
Таким чином, швидкість будь-якої точки твердого тіла, що здійснює обертальний рух, дорівнює добутку кутової швидкості тіла на відстань цієї точки до осі обертання.
Вектор швидкості 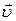 завжди напрямлений по дотичній до кола, яку описує точка, і лежить в площині, перпендикулярній до осі обертання тіла. Інколи швидкість
завжди напрямлений по дотичній до кола, яку описує точка, і лежить в площині, перпендикулярній до осі обертання тіла. Інколи швидкість  точки називають лінійною або коловою швидкістю.
точки називають лінійною або коловою швидкістю.
Проведемо з довільної точки О осі обертання радіус-вектор 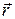 точки М (рис. 23.4), який утворює кут
точки М (рис. 23.4), який утворює кут 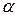 з віссю обертання. З прямокутного трикутника ОСМ виходить:
з віссю обертання. З прямокутного трикутника ОСМ виходить: 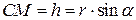 . Тоді
. Тоді
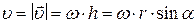
звідкіля, згідно з векторним добутком двох векторів, отримаємо
 . .
| (23.8) |
Тобто вектор швидкості будь-якої точки твердого тіла, що здійснює обертальний рух, дорівнює векторному добутку кутової швидкості тіла, на радіус-вектор цієї точки (формула Ейлера).
При обертальному русі твердого тіла повні прискорення окремих його точок в загальному випадку складаються з тангенціальних 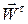 і нормальних
і нормальних 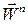 прискорень, алгебраїчні значення яких визначаються за формулами (21.18). Цим формулам можна надати іншого вигляду, якщо використати співвідношення (2.28).
прискорень, алгебраїчні значення яких визначаються за формулами (21.18). Цим формулам можна надати іншого вигляду, якщо використати співвідношення (2.28).
Отримаємо
 , або, кінцево, , або, кінцево, 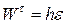 ; ;
| (23.9) |
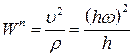 , або, кінцево, , або, кінцево, 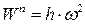 . .
| (23.10) |
Тоді модуль повного прискорення точки
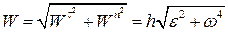 . .
| (23.11) |
Дата добавления: 2016-01-26; просмотров: 1650;
