Теорема. Якщо однорідне тіло має площину, вісь або центр симет­рії, то центр ваги його лежить відповідно в площині, на осі або в центрі симетрії.

Доведення. Якщо тіло симетричне відносно деякої площини П /рис. 17.5/, то кожній частині тіла з одного боку цієї площини відповідає така сама за вагою і симетрично розташована частина з другого боку площини.

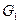Візьмемо яку-небудь частинку А з одного боку площини і знайдемо симетричну їй частинку В з другого боку. На ці частинки діятимуть однакові за модулем сили ваги і 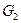.Рівнодіюча 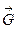цих двох рівних і паралельних сил буде прикладена в точці С - середині відрізка АВ тобто в площині симетрії. Додаючи подібним способом сили ваги

Рис. 17.5
кожної пари симетричних частинок, ми одержимо систему паралельних рівнодіючих сил, що лежать у площині симетрії тіла. У цій самій площині, очевидно, буде лежати і центр ваги тіла.

Коли тіло має вісь симетрії або центр симетрії, теорема доводиться аналогічно.

З цієї теореми випливає ряд окремих випадків, які часто застосовуються на практиці:

І/ центр ваги однорідного тіла обертання лежить на його осі обертання

2/ центр ваги відрізка однорідної матеріальної лінії лежить в його середин і[

З/ центр ваги однорідної пластини /площі/, яка має форму паралелограма /прямокутника, квадрата, ромба/, лежить у точці перетину діагоналей /рис. 17.6/}

4/ центр ваги однорідних пластин, які мають форму правильного многокут­ника, круга, еліпса, лежать в їх гео­метричних центрах; це саме стосується і однорідних тіл, які мають форму кулі, куба тощо.

3. Положення центра ваги простих геометричних ліній, фігур, тіл

Розглянемо деякі приклади на знаходження положення центра ваги деяких простих геометричний ліній, фігур і тіл, які часто зустрічають­ся в інженерній практиці.

Центр ваги площі трикутника.

Якщо позначити координати вершин трикутника через ( )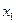

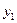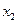
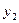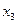
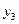( ), ( ), а центр ваги - ( Х_с , Ус),то за формулами аналітичної геометрії для координат точки перетину медіан трикутника матимемо:

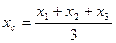
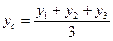/7.23/

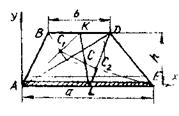
Центр ваги трапеції. Розіб’ємо трапецію ABDE /рис. 17.8/ на еле­ментарні смужки, паралельні основам AЕ і BD. Центри ваги плоских смужок розміщені на прямій KL, яка з’єднує середини основ трапеції. Це означає, що і центр площі трапеції лежить на цій прямій.

Для того щоб знайти, наприклад, ординату Усцентра ваги, можна розбити трапецію на трикутники ABD і ADE, центри ваги яких знаходяться на перетині медіан цих трикутників відповідно в точках С₁ і С_г . Для одержаних трикутників маємо

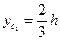
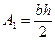
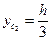
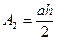
це 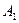і - площі трикутників відповідно ABD і ADE: і - ординати точок С₁ і С_г.

Використовуючи формули /17.17/, одержимо

Рис. 17.8 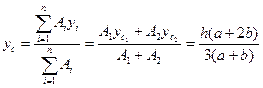/17.24/

Центр ваги площі многокутника.

Для визначення центра ваги довільного многокутника розбиваємо його на трикутники і знаходимо їх центри ваги /рис. 7.9/. Вважаючи вагу кожного трикутника прикладеною в його

центрі ваги, знаходимо центр системи одержаних таким шляхом паралельних сил.

Рис. 17.9