Статичний момент інерції плоскої фігури

Алгебраїчні суми добутків площ частин плоскої фігури на відстань їх центрів ваги до відповідної осі називають статичним моментом інерції площі відносно осей. Отже, статичний момент площі відносно осі у -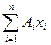

відносно осі х -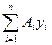

Позначимо статичні моменти площі відносно осей х і у відповідно через 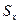і і 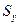приймаючи, що 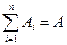- площа всієї плоскої фігури, формули для визначення координат центра ваги матимуть вигляд

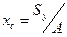
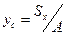/17.19/

Звідси

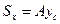
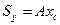/17.20/

тобто статичний момент площі відносно осі дорівнює добутку площі фігу­ри на відстань її центра ваги від цієї осі. Статичний момент плоскої фігури виражається в кубічних метрах, кубічних сантиметрах або кубіч­них міліметрах.

З рівностей /17.20/ витікає, що статичний момент плоскої фігури відносно центральної осі дорівнює нулю. Під центральною віссю розуміють вісь, що проходить через центр ваги плоскої фігури.

Для довільної плоскої фігури /рис. 17.4/ її площу і статичні мо­менти знаходять інтегруванням:

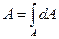
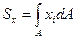
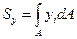/17.21/

де 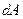- елементарна площадка плоскої фігури»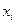 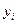- відстань від цієї площадки до відповідної осі; знак А біля інтегралів означає, що інтегрування виконується по всій площі.

Підставивши /17.21/ в /17.20/, дістанемо формули для визначення координат центра ваги довільної плоскої фігури в інтегральній формі:

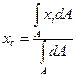
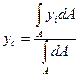/17.22/

Рис.17.4