Загальний випадок дії просторової системи сил на тіло. Головний вектор і головний момент. Рівновага.

Метод зведення сил до одного центра, який розглянуто для плоскої системи сил , можна застосувати і для системи сил, як завгодно розташованих у просторі.

Згідно з теоремою Пуансо , будь-яку силу можна перенести паралельно самій собі в будь-яку точку тіла, додавши при цьому деяку пару. При переносі кожної із сил просторової системи в одну будь-яку довільну точку O /центр зведення/, одержують просторову систему збіжних у цій точці сил і систему приєднаних пар сил, розташованих у різних площинах.

Систему збіжних сил заміняють однією еквівалентною їм силою 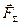, яку називають головним вектором просторової системи сил. Головний вектор 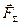дорівнює геометричній сумі всіх даних сил просторової системи, тобто

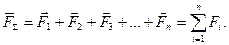/14.3/

Модуль головного вектора визначають за формулою

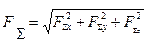/14.4/

Враховуючи, що проекції рівнодіючої на координатні осі x,y,z можна виразити через суму проекцій складових сил на ці самі осі, залежність /14.4/ можна записати у такому вигляді:

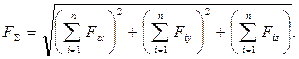/14.5/

Систему приєднаних пар заміняють рівнодіючою парою, момент якої називають головним моментом даної просторової системи сил відносно центра зведення. Головний момент дорівнює геометричній сумі моментів усіх сил відносно точки зведення, тобто

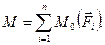/14.6/

Враховуючи /14.2/, знаходять проекції головного моменту на осі координат:

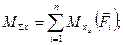
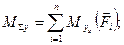
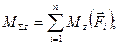/14.7/

Тоді модуль головного моменту визначають за формулою :

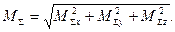/14.8/

Напрям головного вектора і головного моменту знаходять з допомо­гою напрямних косинусів:

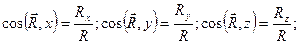
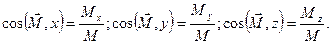
/13.9/

Залежно від значень, які мають головний вектор і головний момент просторової системи сил, можливі такі випадки зведення.

1-й випадок. Головний вектор не дорівнює нулю, а головний момент дорівнює нулю / 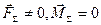/. Система сил зводиться до рівнодіючої, лінія дії якої проходить через центр зведення. Слід зазначити, що рівнодіюча дорівнює і паралельна головному вектору сил. Різниця ж між рівнодіючою сил та їх головним вектором полягає в тому, що рівнодіюча має певне положення лінії дії; положення ж лінії дії головного вектора визначається вибором центра зведення.

2-й випадок. Головний вектор дорівнює нулю, а головний момент не дорівнює нулю / 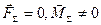/ . Система сил зводиться до пари сил, момент якої дорівнює 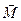і може бути обчислений за /14.8/.

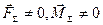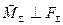3-й випадок. Головний вектор і головний момент не дорівнюють нулю / / і . Система сил також зводиться до рівнодіючої 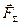, яка не проходить через центр зведенняО , азміщена в точку С ,що лежить на прямій, перпендикулярній до площини, в якій розташовані вектори 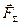і 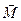.Відрізок 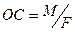. Дійсно, якщо 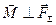,то момент пари, яка зображена вектором 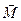, і сила 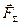лежать в одній площині /рис. 14.4/. Тоді, вибравши сили пари 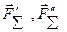рівними за модулем і розмістивши їх так, як показано на рис. 14.4, одержимо, що сили 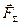і 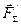взаємно зрівноважуються, і система сил замінюється однією рівнодіючою 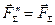, лінія дії якої проходить через точку С. Легко переконатися, що такий випадок буде, зокрема, завжди для будь-якої системи паралель­них сил або сил, що лежать в одній площині, якщо головний вектор .

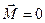4-й випадок. Головний вектор і головний момент не дорівнюють нулю / 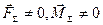/ і при цьому вектор 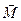паралельний вектору 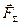/рис. 14.5,а/. Система сил зводиться до сили 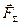і пари 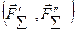, яка лежить у площині, перпендикулярній силі /рис.14.5,б/, де 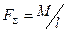. Таку сукупність сили і пари називають динамічним гвинтом, а пряму, вздовж якої напрямлений вектор 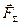- віссю гвинта. Подальше спрощення цієї системи неможливо.

5-й випадок. Головний вектор і головний момент не дорівнюють нулю / 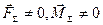/ і при цьому вектори 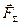і 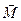не перпендикулярні між собою і не паралельні /рис. 14.6,а/. Система сил також зводиться до динамічного гвинта, але вісь гвинта не буде проходити через центр О.

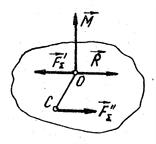
Рис. 14.4

Рис. 14.5

Рис. 14.6

6-й випадок. Головний вектор і головний момент дорівнюють нулю. Система сил зрівноважена. Векторні рівняння

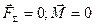/14.10/

виражають необхідну і достатню умови рівноваги просторової системи довільно розташованих сил.

Таким чином, для рівноваги просторової системи довільно розташованих сил необхідно і достатньо, щоб дорівнювали нулю головний вектор цієї системи і головний момент відносно довільно вибраного центра зведення.

Якщо головний вектор дорівнює нулю, то його проекції на три взаємно перпендикулярні осі також дорівнюють нулю. Аналогічно, якщо головний момент дорівняє нулю, то дорівнює нулю і сума моментів всіх сил відносно цих осей. Тому маємо:

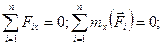
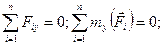
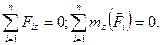/14.11/

Отже, для рівноваги системи сил, розташованих як завгодно у просторі, необхідно і достатньо, щоб сума проекцій усіх сил на кожну з трьох координатних осей і алгебраїчна сума їх моментів відносно цих осей дорівнювали нулю.