Просторова система збіжних сил
План
1. Рівнодійна просторової системи збіжних сил
2. Визначення реакцій опори стержньових систем.
ЛІТЕРАТУРА ОСНОВНА
ЛІТЕРАТУРА ДОДАТКОВА
Студенти повинні знати: Визначення головного вектора просторової системи збіжних сил. Геометричну та аналітичну умову рівноваги просторової системи збіжних сил.
Студенти повинні вміти: Складати та розвязувати рівняння рівноваги для просторової системи збіжних сил
3. Рівнодійна просторової системи збіжних сил
В багатьох випадках практики всі сили, що діють на будь які механізми, споруди мажна звести до плоскої системи сил. Часто просторова система сил може бути замінена декількома плоскими системами сил.
Але це не завжди. Тому в статиці приходиться вивчати зведеня та рівновагу системи сил, що нележить в одній площині, тобто просторову систему сил.
Система сил, лінії дії яких не лежать в одній площині, але перетинаються в одній точці, називається просторовою системою збіжних сил. Рівнодіючу просторової системи збіжних сил можна визначити, побудувавши силовий многокутник /рис. 13.1 а /.
Модуль рівнодіючої просторової системи збіжних сил можна визначити аналітично, використавши метод проекцій.
Суміщаємо початок координат з точкою перетину ліній дій сил системи. Проецируємо всі сили на осі координат і додаємо відповідні проекції /рис. 13.1 б /. Отримаємо проекції рівнодіючої на вісі: 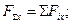
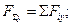
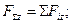
Модуль рівнодіючої сили можна знайти за рівнянням:
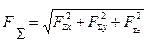
Напрямок вектора рівнодіючої визначається кутами:
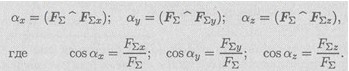
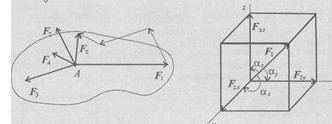
а/ б/
Рис. 13.1
Геометрична умова рівноваги . Оскільки головний вектор системи збіжних сил визначається як замикаюча сторона силового многокутника, то обертається в нуль тоді, коли багатокутник буде замкненим Отже: для рівноваги системи збіжних сил необхідно і достатньо, щоб силовий многокутник, що побудований з цих сил, був замкненим.
Аналітична умова рівноваги виражається рівняннями:

Тобто для рівноваги просторової системизбіжних сил необхідною та достатньою умовою є те, що сума проекцій всіх сил системи на три взаємноперпендикулярні осі дорівнює нулю. / рис. 10.2/

Рис. 13.2
Теорема Варіньона
(терема про момент рівнодіючої збіжної системи сил)
Момент рівнодіючої системи збіжних сил відносно довільного просторового центра дорівнює векторній сумі моментів сил складових відносно того ж центра.
Розглянемо просторову систему збіжних сил 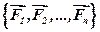 , лінії дії яких перетинаються в точці С (рис.13.3)
, лінії дії яких перетинаються в точці С (рис.13.3)
З довільно обраного моментного центра А проведемо до точки сходу С радіус-вектор 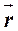 і підсумуємомоменти кожної сили відносно центра А:
і підсумуємомоменти кожної сили відносно центра А:

Рис.13.3
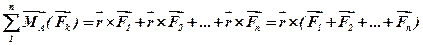 .
.
Але 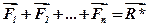 і тому
і тому 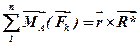 , або
, або 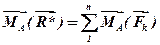 , що і потрібно було довести.
, що і потрібно було довести.
Теорема Варіньона справедлива не тільки для систем збіжних сил, вона узагальнюється і на будь-яку систему сил, що зводиться до рівнодіючої.
Для плоскої системи збіжних сил теорема формулюється так: момент рівнодіючої відносно точки площини, де розташована система сил, дорівнює алгебраїчній сумі моментів складових відносно тієї ж точки. Тобто:
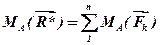 .
.
Дата добавления: 2016-01-26; просмотров: 4419;
