Пара сил і її властивості

Парою сил називають систему двох рівних за модулем паралельних сил, напрямлених в протилежні сторони по паралельних лініях дії (рис.6.2).

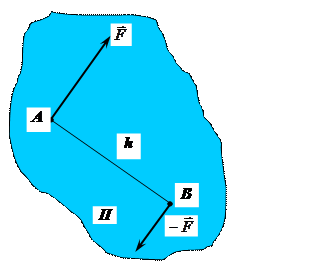
Рис.6.2

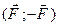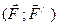Пару сил позначають так: або . Площину, в якій розташовані паралельні сили, називають площиною дії пари сил, чи, просто, площиною пари.

Вперше поняття пари сил – нової абстракції в механіці – було введено Луї Пуансо (1777-1859) академіком Паризької академії наук у 1803 р. в трактаті "Початки статики".

Пара сил не утворює зрівноважену систему і не має рівнодіючої. Вона не може бути спрощена і тому є особливою мірою механічної дії на дане тіло з боку інших тіл. Досвід показує, що пара сил, прикладених до твердого тіла, прагне надати йому певне обертання. Цей обертальний ефект пари сил оцінюється моментом пари сил.

Момент пари сил

Нехай дано пару сил 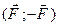, що діє в площині N, розташованій як завгодно у просторі. Обчислимо суму моментів сил 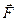і 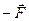, що складають пару, відносно довільного центра О. З’єднаємо початки сил з цим центром радіусами-векторами 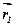і 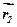. Згідно з визначенням вектор-момента сили (формула 6.1), будемо мати:

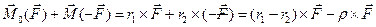(6.4)

Отриманий результат не залежить від положення центра О, відносно якого визначено момент пари сил, тобто вектор-момент сил пари є вільним вектором. У подальшому позначатимемо його через 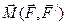, або скорочено 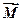. Тоді:

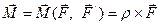(6.5)

Таким чином, момент пари сил – це вільний вектор , напрямлений перпендикулярно до площини дії пари в той бік, звідкіля обертання тіла під дією пари сил відбувається проти руху годинникової стрілки (рис.6.3).

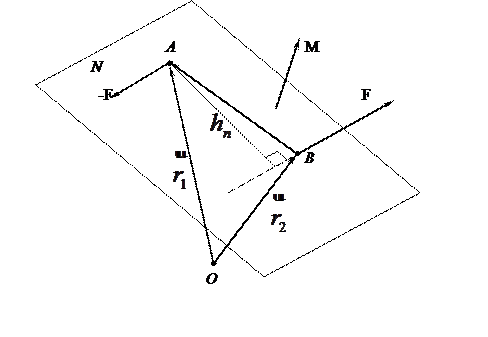
Рис.6.3

Напрям векто­ра моменту пари сил можна знайти за правилом гвинта /шурупа/ з правою різьбою. Напрям руху гвинта при його загвинчуванні або відгвинчуванні показує напрям дії вектора моменту пари сил. Дійсно, якщо загвинчувати гвинт в тіло /гайку/, ми повинні повертати його за рухом годинникової стрілки, при цьому гвинт руха­тиметься від нас; і навпаки, якщо викручуватимемо гвинт, то його треба повертати проти руху годинникової стрілки.

Модуль момента пари сил дорівнює добутку модуля однієї з сил пари на плече пари h_n, тобто на найкоротшу відстань між лініями дії сил, що складають пару:

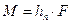(6.6)

Ефект дії пари залежить від величини сили 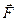і довжини плеча h_n . Як показує досвід, чим більша сила 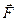і більше плече h_n, тим більший обертальний ефект пари сил на тіло.

Домовимося вважати момент пари сил додатним /знак "+"/, якщо пара намагається повернути тіло проти обертання годинникової стрілки; якщо ж пара намагається повернути його у напрямі обертання годинни­кової стрілки - від’ємним /знак "-"/.

У Міжнародній системі одиниць /СІ/ момент пар виражається в ньютонометрах /Н·м/ або кілоньютонометрах /кН·м/, оскільки сила вира­жається в ньютонах /Н/ або кілоньютонах /кН/, а довжина плеча - у метрах /м/.

Теорема Варіньона

(терема про момент рівнодіючої збіжної системи сил)

Момент рівнодіючої системи збіжних сил відносно довільного просторового центра дорівнює векторній сумі моментів сил складових відносно того ж центра.

Розглянемо просторову систему збіжних сил 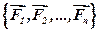, лінії дії яких перетинаються в точці С (рис.4.5)

З довільно обраного моментного центра А проведемо до точки сходу С радіус-вектор 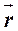і підсумуємомоменти кожної сили відносно центра А:

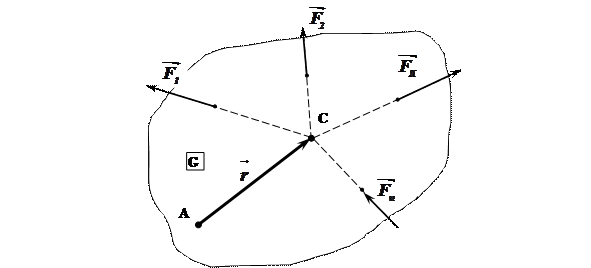
Рис.4.5

.

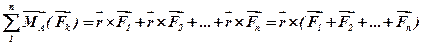Але 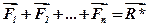і тому 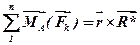, або 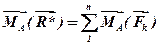, що і потрібно було довести.

Теорема Варіньона справедлива не тільки для систем збіжних сил, вона узагальнюється і на будь-яку систему сил, що зводиться до рівнодіючої.

Для плоскої системи збіжних сил теорема формулюється так: момент рівнодіючої відносно точки площини, де розташована система сил, дорівнює алгебраїчній сумі моментів складових відносно тієї ж точки. Тобто:

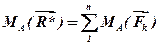
Питання для самоконтролю

1. Що називають парою сил?

2. Чим оцінюється обертовий ефект пари, сил?

3. В яких одиницях вимірюється момент пари сил?

4. Як визначають напрям вектора моменту пари сил?

5. Дайте визначення векторного момента сили відносно довільного просторового центра і наведіть відповідну формулу.

6. Визначить геометричні місця точок простору, відносно яких моменти даної сили : а) геометрично рівні; б) рівні за модулем.

7. Що називають плечем сили?

8. Дайте визначення алгебраїчного момента сили відносно точки площини, в якій розташована лінія дії сили.

9. В яких випадках момент сили відносно а) довільного просторового центра; б) осі; в) точки площини, в якій розташована лінія дії сили, дорівнює нулю?

10. Чи можуть бути рівними моменти двох різних сил відносно однієї точки площини?

11. Дайте визначення пари сил. Чому дорівнює момент пари сил?

Заняття № 7

Тема: Пара сил.

План

1. Властивості пар. Додавання пар. Еквівалентність пар. Умова рівноваги.
2. Розв’язання задач на визначення моментів сил і пар.

ЛІТЕРАТУРА ОСНОВНА

ЛІТЕРАТУРА ДОДАТКОВА

Студенти повинні знати: Визначення моменту пари сил та сили відносно точки, теореми про властивості пар, правило додавання пар.

Студенти повинні вміти: визначати моменти пар сил та сил відносно точки, додавати моменти пар і сил.