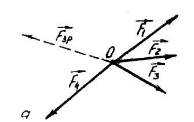
Визначення модуля і направлення рівнодіючої двох сил, прикладених в одній точці.

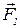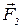Найпрості­шою плоскою системою збіжних сил є дві сили і /рис. 3.3,а/, які прикладені в одній точці О.

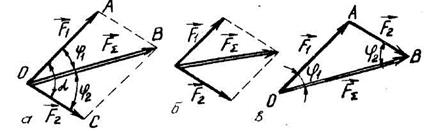
Рис. 3.3

Геометричну суму двох збіжних сил - рівнодіючу 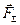- знаходять згідно з четвертою аксіомою статики за правилом паралелограму /рис. 3.3,а/ чи правилом трикутника /рис. 3.3,в/. Якщо сили 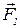і 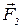рівні між собою, то паралелограм ОАВС стає ромбом /рис. 3.3,б/.

При графічному методі визначення рівнодіючої вектори сил 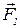і 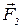відкладають в одному масштабі, кути a, 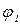і 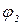/рис. 3.3,а/ залишаються незмінними, вони не залежать від масштабу побудови сил. Під масштабом сил 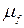розуміють відношення модуля сили 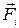до довжини відрізка 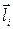, який зображує цю силу на рисунку, тобто

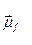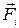= /l ( 3.1 )

Масштаб 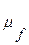показує число одиниць сили в ньютонах /Н/ або кілоньютонах /кН/ в одиниці довжини відрізка /мм/, тому його одиниця є ньютон на міліметр /Н/мм/, кілоньютон на міліметр /кН/мм/ і т. ін.

Користуючись залежністю /3.1/, можна визначити модуль сили, що зображена на . рисунку ( 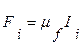),або довжину відрізка 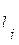, що зображує силу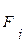 на рисунку у заданому масштабі )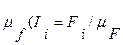

Розкладання сили на дві складові. Правило силового паралелогра­ма можна використати при розкладанні сили на дві складові, рівнодію­ча яких повинна дорівнювати заданій силі. Зрозуміло, що коли можна дві збіжні сили 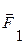і 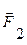/рис. 3.3/ замінити однією силою 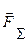/рів­нодіючою/, то, навпаки, дію однієї сили 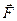завжди можна замінити дією двох сил 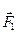і 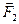, які перетинаються на лінії дії заданої сили. При цьому необхідно, щоб сила 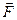за модулем і напрямом була діагонал­лю паралелограма, сторонами якого служать сили 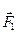і 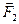/рис. 3.4/.

Враховуючи, що на заданій діагона­лі 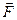можна побудувати нескінченну кількість паралелограмів, а тому, щоб розв'язок був визначений, не­обхідно задати додаткові умови:

а/ напрями дії сил 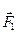і 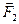/лі­нії дії ОМ і ON/; б/ напрям і модуль однієї із складових сил;

в/ модулі обох складових сил; г/ модуль однієї складової сили і напрям другої. 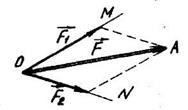Рис. 3.4

Геометричний метод, визначення рівнодіючої сили /метод силового многокутника/. Розглянемо загальний випадок плоскої системи збіжних сил, приклад якого показано на рис. 3.5,а. Для додавання сил 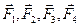можна використати метод силового трикутника. Додаючи на під­ставі цього методу дві сили 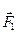і 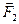/рис. 3.5,б/, одержимо їх рівно­діючу, яку позначимо 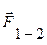, що відповідає векторному рівнянню /гео­метричній сумі/

Потім знаходимо геометричну суму 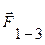, двох інших векторів

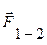і :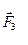

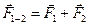(3.2 )

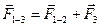( 3.3 )

і, зрештою, знаходимо геометричну суму векторів сил 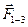і :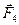

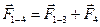(3.4 )

Підставляючи у рівнян­ня /3.4/ залежності /3.3/ і /3.2/, маємо:

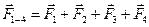; (3.5 )

У загальному вигляді залежність /3.5/ записується:

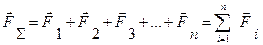; (3.6 )

Таким чином, рівнодіюча плоскої системи збіжних сил дорівнює їх векторній /гео­метричній/ сумі.

Аналізуючи рис.3.5,б, можна побачити, що для зна­ходження рівнодіючої 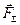необов'язково визнавати проміжні складов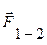і і 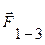і т.ін., достатньо від кінця вектора 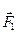від­класти вектор 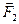/рис. 3.5,в/, від кінця_ вектора 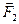- вектор 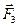і т.д. Тоді рівнодіюча 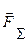визначатиметься відрізком, який з’єднує початок пер­шої сили 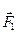з кінцем остан­ньої сили , і матиме на­прям від початку першої сили до кінця останньої. Фігуру, яку ми одержали /рис. 3.5,в/, називають силовим многокутником, або планом сил. Силовий многокутник будується у масштабі .

Необхідно звернути увагу на те, що складові 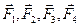силового многокутника напрямлені в один бік обходу контура ABCDE, а рівнодіюча 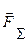- у протилежний. Крім цього, неважко показати, що послідовність побудови сторін силового многокутника не впливає на

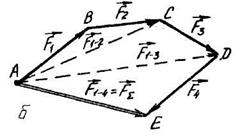
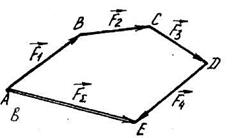
Рис. 3.5

остаточний результат тобто, якщо поміняти місцями 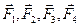сили то величина і напрям рівнодіючої не зміниться /від перестановки доданків сума не змінюється/.

Умови рівноваги системи збіжних сил. Як ми вже побачили, рівно­діюча 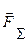замінює систему збіжних сил. Тому, визначивши рівнодіючу збіжних сил, легко розв’язати задачу про зрівноваження цієї системи сил. Для цього необхідно додати до заданої системи сил 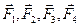ще одну силу, яка чисельно до­рівнює рівнодіючій 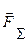, але напрямлена у протилежний бік /рис. 3.5,а/, тобто зрівноважуючу силу 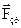. Силовий многокутник, який побудовано для системи сил, що знаходяться в рівновазі, буде замкнутим /рис. 3.6/. Векторна сума таких сил дорівнює нулю тобто

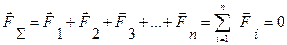
(3.7)

Інакше, для рівноваги плоскої системи збіжних сил необхідно і достатньо, щоб геометрична сума заданих сил /рівнодіюча/ дорівнюва­ла нулю.

Геометрична умова рівноваги використовується при розв'язанні задач графічним

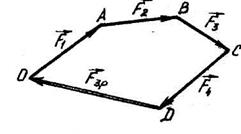
Рис. 3.6

методом. Якщо система збіжних сил знаходиться в рівновазі, то силовий многокутник є замкнений.

Інакше, для рівноваги плоскої системи збіжних сил необхідно і достатньо, щоб геометрична сума заданих сил /рівнодіюча/ дорівнювала нулю.

Питання для самоконтролю

1. Яка система сил називається збіжною?

2. Які є системи збіжних сил? Наведіть приклади найпростіших систем збіжних сил /плоскої і просторової/.

3. Сформулюйте правила побудови силового трикутника, паралело­грама, паралелепіпеда і многокутника.

4. Графічна умова рівноваги плоскої та просторової систем збіжних сил.

5. Чи може вільне тверде тіло знаходитися в рівновазі під дією а/ однієї сили; б/ двох сил; в/ трьох сил?

6. Яку фігуру утворює силовий многокутник, побудований для плос­кої зрівноваженої системи збіжних сил, що однакові за модулем, і складаються а/ з трьох сил, б/ чотирьох сил, в/ п’яти сил тощо?

7. Яку фігуру утворює паралелепіпед сил, побудований для трьох збіжних, взаємно перпендикулярних і рівних за модулем сил?

Заняття № 4