Сила, сила як вектор, одиниці вимірювання сили, сила тяжіння.
Система сил, еквівалентні системи. Рівнодіюча сила. Врівноважуюча сила. Зовнішні і внутрішні сили.
Силою називають міру механічної взаємодії між тілами, в результаті якої змінюються відносне положення тіл, їх швидкості та форма.
Сила - величина векторна і визначається трьома елементами: числовим значенням /модулем/, напрямом дії, точкою прикладання /місцем контакту взаємодіючих тіл/.
За одиницю сили в Міжнародній системі одиниць /СІ/ прийнятий ньютон /Н/. Часто використовують кратні одиниці – кілоньютон І кН = І03 Н/ або меганьютон /І МH = 106 Н/. У технічній системі одиниць прийнято кілограм-силу /кгс/.
Для порівняння: І Н = 0,102 кгс; І кгс = 9,81 Н.
Під напрямом сили розуміють напрям того руху, який дістало б вільне тіло, що перебуває у стані спокою, якби на нього подіяла ця сила.
Якщо сила прикладена до твердого тіла, то вона є пересувним вектором. Початок пересувного вектора може бути пересунутий вздовж лінії його дії. Узадачах опору матеріалів, коли має значення точка прикладання сили, вона є вектором означеним.
Пряму, вздовж якої напрямлений вектор сили, називають лінією дії сили.
Надалі вектори сил позначатимемо латинськими буквами (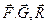 
) і ін. зі стрілками зверху. Модуль сили позначається такими самими буквами, але без стрілок ( F, G, R ).
Як і всякий вектор, силу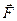 
можна зобразити графічно у вигляді напрямленого відрізка AB /рис. 2.1/. Точку A називають початком вектора, а точку B - його кінцем. Стрілка на кінці вектора показує напрям дії сили.
Системою сил називають сукупність сил, що діють на одне тверде тіло.
Розрізняють такі види систем сил: система сил, що діють вздовж однієї прямої лінії; система збіжних сил; система паралельних сил; система довільно розташованих сил.
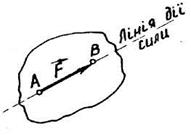
Рис. 2.1
Еквівалентними системами сил називають дві системи сил, які однаково діють на одне і те саме тіло. Тобто, якщо одну систему сил, яка прикладена до твердого тіла, замінити іншою, їй еквівалентною системою, то механічний стан тіла не зміниться.
Рівнодіючою силою називають одну силу, яка еквівалентна даній системі сил. Рівнодіючу силу позначають 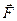Σ , Знаходження рівнодіючої сили називають додаванням сил. Зворотню дію, тобто заміну однієї сили еквівалентною системою сил, називають розкладанням сили.
Зрівноваженою системою сил називають таку систему сил, під дією якої тіло не змінює свого руху або залишається у стані спокою.
Зрівноважуючою силоюназивають силу, яка, при прикладенні до системи сил, приводить її до рівноваги.
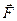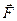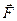Зрівноважуюча сила зр дорівнює за модулем рівнодіючій силі і напрямлена по лінії її дії у протилежний бік, тобто Σ= - зр.
Під рівновагою твердого тіла розуміють такий механічний стан тіла, за якого воно рухається по інерції.
Простішими прикладами інерційного руху є прямолінійний рівномірний рух точки, прямолінійний рівномірний поступальний рух тіла, рівномірний обертальний рух тіла навколо нерухомої осі. Окремим випадком руху по інерції є стан спокою.
Щоб визначити, знаходиться тіло у стані рівноваги чи ні, треба домовитися про систему відліку, відносно якої розглядається положення тіла. Такою системою відліку, яка має назву інерціальної, або галілеєвої /по імені Галілея, який вперше установив закони руху/, є система відліку, пов’язана з Землею або Сонцем.
Усі сили, що діють на механічну систему, поділяють на дві групи: зовнішні та внутрішні.
Зовнішніми називають сили, що діють на тверде тіло з боку інших тіл.
Внутрішніми називають сили взаємодії між точками даного тіла.
3. Аксіоми статики
В основі вчення про рівновагу абсолютно твердих тіл лежать деякі прості положення, що є постулатами, або аксіомами, статики. Ці аксіоми сформульовані в результаті спостереження і вивчення навколишніх явищ реального світу. Деякі основні закони механіки, відкриті Галілеєм і Ньютоном, є одночасно і аксіомами статики.
Аксіома 1 /принцип інерції/. Всяка матеріальна точка /тіло/ перебуває у стані спокою або рівномірного прямолінійного руху доти, поки прикладені сили не виведуть її з цього стану.
Цю аксіому, яку сформулював уперше І.Галілей, називається принципом /законом/ інерції, оскільки прямолінійний і рівномірний рух тіла, що відбувається без дії сил, називається рухом по інерції /від латинського " inertia - бездіяльність/. І.Ньютон узагальнив висновки Г.Галілея і включив їх до числа основних законів механіки /перший закон Ньютона/.
Інакше, ізольована матеріальна точка перебуває у стані спокою або рухається прямолінійно рівномірно, тобто знаходиться у рівновазі.
Ізольованою матеріальною точкою називають точку, на яку не діють інші тіла.
Закон інерції зовсім не очевидний, як це може здаватися з першого погляду. Протягом віків вважали, що коли немає зовнішнього впливу на тіло, то воно може перебувати тільки в стані спокою, що спокій - це ніби природний стан тіла. А щоб тіло рухалося зі сталою швидкістю, на нього повинно діяти інше тіло, здавалося б, це підтверджується повсякденним досвідом: щоб віз рухався з постійною швидкістю прямою горизонтальною дорогою, його повинен весь час тягти кінь. Але це потрібно тільки для того, щоб компенсувати цю силу тертя. Галілей зробив висновок, що коли б не було тертя, тіло, приведене в рух, продовжувало б рухатися з постійною швидкістю і без зовнішньої дії.
Крім цього, з першого закону Ньютона можна зробити такий висновок: якщо тіло не знаходиться у спокої або не рухається рівномірно і прямолінійно /по інерції/, то на нього діють інші тіла /зовнішні сили/. Ця дія може здійснюватись або шляхом безпосереднього контакту між тілами /тепловоз тягне вагони, будівля тисне не фундамент/, або на відстані /Земля притягує супутник, Сонце притягує Землю та інші планети, магніт або електричний струм відштовхує або притягує ошурки тощо/.
Аксіома 2 /умова рівноваги двох сил/. Дві сили, прикладені до твердого тіла, урівноважуються тоді і тільки тоді, коли вони рівні за величиною /модулем/ і діють по одній прямій у протилежні боки /рис. 2.2/.
Цією аксіомою встановлюється найпростіша система зрівноважених сил, що еквівалентні нулю. Дія врівноваженої системи сил на тіло не змінює механічного стану тіла
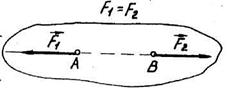
Рис. 2.2
/стану спокою або рівномірного й прямолінійного руху/. Аксіома справедлива і для абсолютно твердого тіла і матеріальної точки; для тіла, яке може деформуватися, вона не завжди справедлива.
Аксіома 3 /принцип приєднання і відкидання зрівноважених сил/. Дія даної системи сил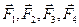 
на тверде тіло не зміниться, якщо до неї додати або від неї відняти зрівноважену систему сил. Інакше кажучи, якщо до даної системи сил 
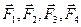/рис. 2.З/ приєднати зрівноважені сили 
=- 
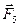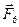
/зображені штриховою лінією/ або з даної системи сил їх виключити, то знову одержимо систему сил, еквівалентну заданій. Під дією даної системи сил
( 
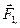
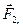
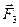
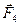) і нової( 
, 
, , , 
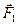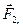
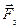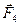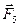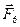) тіло буде рухатись /або знаходитися в стані спокою/ так само / за інших рівних умов/. Зокрема, до будь-якої системи сил можна додавати або віднімати найпростішу зрівноважену систему сил, що складається з двох рівних за модулем сил, напрямлених у різні боки і прикладених в одній або різних точках твердого тіла. Цей прийом часто використовується при розв’язанні задач механіки.
Наслідок1 /теорема про ковзний вектор сили/. Дія сили на тверде тіло не зміниться, якщо перенести цю силу по лінії її дії в будь-яку точку.
Необхідно зазначити, що перенесення сили вздовж її лінії дії можливе тільки в статиці твердого тіла. У тілах, які деформуються, така операція може різко змінити характер деформації. /Див. рис. 2.4/
Аксіома 4 /правило паралелограма сил/. Рівнодіюча двох сил, прикладених в одній точці, прикладена в тій самій точці і зображується діагоналлю паралелограма, що побудований на цих силах як на сторонах. На рис. 2.5 система двох сил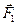 
і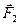 
має рівнодіючу 
.
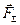Математично операції визначення рівнодіючої двох сил 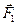і 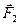можна записати у вигляді векторного рівняння
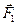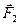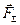+ = . / 2.1/
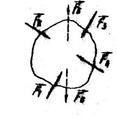
Рис. 2.3
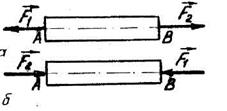
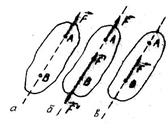
Рис. 2.4
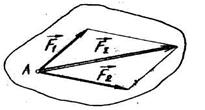
Рис. 2.5
Сума, виражена / 2.І /, називається векторною, або геометричною.
Отже, можна сказати, що рівнодіюча двох сил, прикладених в одній в точці, дорівнює векторній /геометричній/ сумі цих сил. І
Правило додавання двох сил, обумовлене четвертою аксіомою, називається правилом паралелограма.
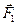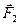Якщо дві сили і прикладені до різних точок тіла, лінії дії яких лежать в одній площині, тобто перетинаються в одній точці О; /рис. 2.6/, то, знаючи, що сила це ковзний вектор, можна сили F 1 і F 2 з точок A і В перенести в точку О їхнього перетину, а потім подати за правилом паралелограма. \
З правила паралелограма можна одержати друге правило додавання двох сил, що діють на тіло в одній площині /рис. 2.6/ - правило трикутника.
Правилом силового паралелограма можна скористатися і для розв'язання зворотної задачі - розкладання даної сили на дві складові, що прикладені в цій самій точці O /рис, 2.7/. Тут достатньо на заданому векторі сили, як на діагоналі, побудувати паралелограм сил, напрями яких також задані. Сторони цього паралелограма і будуть складовими силами.
Наслідок 2 /теорема про три сили/. Якщо тверде тіло знаходиться у рівновазі під дією трьох непаралельних сил і лінії дії двох сил перетинаються, то всі три сили лежать в одній площині, а лінії дії цих сил перетинаються в одній точці. / Рис, 2.8 /
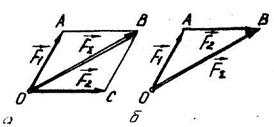
Рис. 2.6
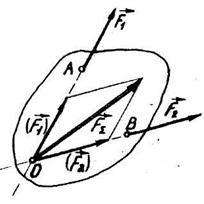
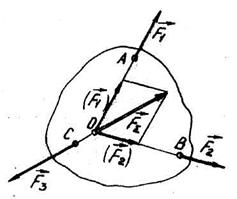
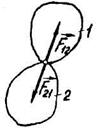
Рис. 2.7 Рис. 2.8
Рис. 2.9
Аксіома 5 /закон дії і протидії/. Сили, з якими діють одне на одне два тіла, завжди рівні за модулем і напрямлені по одній прямій у протилежні боки /рис. 2.9/. Інакше: дії завжди відповідає рівна їй, але протилежна за напрямом протидія.
Цей закон відомий у фізиці як третій закон Ньютона і називається законом рівності дії і протидії. Якщо на тіло І діє тіло 2 силою 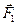, то на тіло 2 діє тіло І з такою самою силою 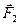, яка напрямлена в протилежний бік. Хоча сили 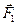, 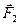рівні за модулем і діють вздовж однієї прямої у протилежні боки, вони не зрівноважують одна одну, оскільки прикладені до різних тіл.
Аксіома 6 /принцип затвердіння/. Якщо нетверде тіло /тіло, що може деформуватися/ знаходиться в рівновазі, то ця рівновага не порушиться і тоді, коли тіло стане абсолютно твердим.
Дата добавления: 2016-01-26; просмотров: 6498;