Тема: Плоска система збіжних сил.

План

1. Проекція сили на вісь, правило знаків. Проекції сили на дві взаємно перпендикулярні вісі.

2. Аналітичне визначення рівнодіючої плоскої системи збіжних сил (метод проекції).

3. Аналітична умова рівноваги плоскої системи збіжних сил (рівняння рівноваги). Стержневі системи з ідеальними шарнірами.

ЛІТЕРАТУРА ОСНОВНА

ЛІТЕРАТУРА ДОДАТКОВА

Студенти повинні знати: Визначення проекції сили, одиниці вимірювання, аналітичну умову рівноваги системи збіжних сил.

Студенти повинні вміти: Визначати проекцію сили на ось, суму проекцій системи збіжних сил , вміти складити і розвязувати равняння рівноваги системи збіжних сил.

Аналітичний метод визначення рівнодіючої /метод проекцій/. Гра­фічний метод визначення рівнодіючої недостатньо точний, тому частіше для визначення рівнодіючої системи збіжних сил і розв'язання інших задач статики використовують метод проекцій сили на координатні осі /аналітичний метод/.

Проекцією вектора 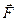на вісь називають відрізок ab /рис. 4.1/ цієї осі, який знаходиться між двома перпендикулярами, що опущені на цю вісь з початку і кінця вектора 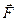. Отже, проекція сили на вісь не є вектором. Це величина скалярна, алгебраїчна. Проекцію сили 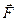на вісь позначатимемо такою самою лі­терою F з доданням індексу, яким позначено вісь, на яку сила проекціюється. У даному випадку /рис. 4.1/ проекцію сили 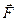на вісь X позначимо Fx.

Величину проекції Fx сили 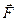можна знайти з трикутника ABC /рис. 4.1/. Якщо врахувати, що у цьому трикутнику сторона AC=ab =Fx то одержимо:

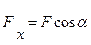( 4.1 )

Отже, проекція вектора сили на будь-яку вісь дорівнює добут­ку модуля цієї сили на косинус кута між напрямом сили і додатним напрямом осі.

Рівність /4.1/ у всіх ви­падках визначає не тільки числове значення проекції, але й її знак. Якщо кут 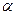гострий / 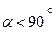/, то проекція додатна; для тупого кута

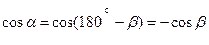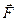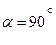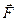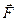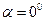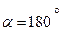/рис. 4.1,б/ проекція Fx від'єм­на. Якщо сила перпендикулярна до осі / /, її проекція на цю вісь дорівнює нулю /рис.4.1,в/. У даному випадку і початок, і кі­нець сили проектуються в одну і ту саму точку /точки a і b збігаються/. Якщо сила паралельна осі / або /, то вона проектується на цю вісь у нату­ральну величину /рис. 4,1, г,д/, причому Fх =F / / або Fх =-F / /.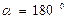

Проекції сили на координатні осі. Якщо задані вектор сили і на­прям осі, то проекція цього вектора на вісь визначається однозначно. Проте, знаючи проекцію вектора на вісь, не можна визначати сам век­тор, тому що різні вектори можуть мати однакові проекції на цю вісь /рис. 4.2/. Для визначення вектора треба знати принаймні його проекції на дві непаралельні осі.

Рис. 4.1

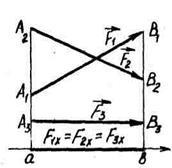Зазвичай, у площині, в якій лежить вектор, вибирають дві взаємно перпендикулярні осі 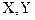/ рис. 4.2/ осі плоскої прямокутної системи координат.

Рис. 4.2

На рис. 4.3 показана прямокут­на система координат з осями X і Y, на якій зображена задана сила 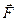.Спроеціюємо цю силу на осі X і Y. Для цього поставимо через точки А і В / початок і кінець вектора/, перпендикуляри до осей X і Y, одержимо відрізки а₁в₁ і а₂в₂., які будуть зображати відповідні проекції сили 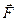на ці вісі. Розглядаючи трикутники АВС і АDB, можна записати:

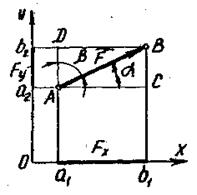Рис. 4.3

Проекцією вектора на 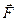на осі 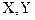є відповідно відрізки:

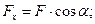
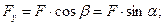(4.2 )

Де 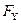= а₁ в₁ = АС; 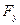= а₂ в₂ = АD - проекції вектора 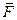відповідно на осі X і Y.

Тепер поставимо обернену задачу: знаючи проекції сили, визначити величину і напрямок даної сили.

Величина /модуль/ сили 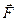визначається з трикутника АВС або АВD /рис. 2.9/ за теоремою Піфагора:

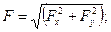(4.3 )

У цій формулі треба брати арифметичне /додатне/ значення коре­ня, тому що модуль вектора 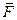є величина додатна.

Напрям сили 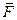визначають напрямними косинусами

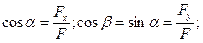( 4.4 )

Або 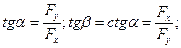( 4.5 )

Обчисливши значення тригонометричних функцій, знаходимо кут α або β, який утворює сила 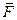з додатним напрямом осі X /або віс­сю Y/.

Отже, використовуючи формули /4.4 /, /4.5/, можна визначити ве­личину і напрям сили за її проекціями на осі координат.

Визначення рівнодіючої методом проекцій. Раніше ми показали, що рівнодіюча плоскої системи збіжних сил зображується замикаючою сто­роною силового многокутника /див. рис. 3.5/. Спроеціюємо цю рівно­діючу і всі складові сили на будь-яку вісь, наприклад на вісь X /рис. 4.4/.

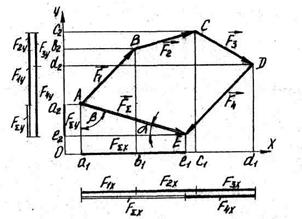Рис 4.4

З рис 4.4 видно, що

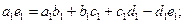
отже, якщо врахувати, що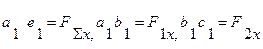

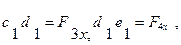де F _Σx , F _1x, F_2x, F_3x,F_4x

відповідно проекції рівнодіючої сили 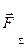і сил 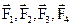на вісь X, то можна записати

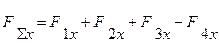( 4.6 )

У загальному вигляді залежність /4.6/ записується

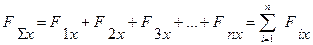( 4.7 )

На підставі рівняння /4.7/ можна зробити висновок, що проекція рівнодіючої на будь-яку вісь дорівнює сумі проекцій складових сил на цю саму вісь.

Очевидно, що цей висновок може бути узагальненим на будь-яку кількість сил і на будь-яку ось. Тому проекція рівнодіючої сили на вісь Y (рис. 4.3/ виражатиметься рівнянням 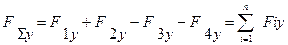( 4.8 )

де 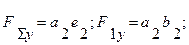F _2y=b ₂c ₂ , F_3y=c₂d₂ , F_4y=d₂е₂

Знайшовши проекції рівнодіючої на осі Л і Q визначають мо­дуль рівнодіючої сили:

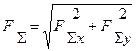( 4.9 )

її напрям визначається напрямними косинусами

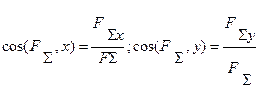( 4.10 )

Рівняння рівноваги системи збіжних сил. Умова рівноваги системи збіжних сил в аналітичній формі випливає з умови /4.9/. Дійсно, якщо рівнодіюча зрівноваженої системи сил 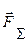= 0, то і її проекції на осі координат .

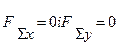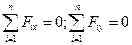Таким чином, для рівноваги плоскої системи збіжних сил необхід­но і достатньо, щоб алгебраїчна сума проекцій усіх сил системи на кожну з двох осей координат дорівнювала нулю. Рівняння рівноваги у цьому випадку мають такий вигляд:

( 4.11 )

. (4.12)