Вільне і невільне тіло. В'язі. Реакції ідеальних в'язей та визначення їх напрямків.
В механіці тіла поділяються на вільні та невільні.
Вільними називають такі тіла, які мають можливість здійснювати будь-який рух у просторі, для цього досить прикласти відповідну силу.
Тіло називають невільним, якщо його переміщення у просторі обмежене якимись іншими тілами /вантаж, підвішений на тросі підйомного крану, вагонетка, яка рухається по рейках; балка, що спирається на опори, і т. ін./.
В’яззю називають всі ті матеріальні об’єкти, які обмежують рух даного твердого тіла в росторі.
Сила, з якою в’язь діє на тіло, заважаючи переміщенню цього тіла,називається реакцією в’язі.
Надалі сили, які не є реакціями в’язей (такі, що сприяють руху тіла,як, наприклад, сила ваги), будемо називати активними силами.
Аксіома про звільнення від в’язей стверджує, що невільне тверде тіло можна розглядати як вільне, якщо дію в’язей замінити реакціями в’язей.
Тіла, що обмежують свободу переміщення даного тіла, називають в'язями. Так, в наведених прикладах в’язями є відповідно трос, рейки, опори балки. Тоді можна сказати, що невільними є тіла, на які накладені в’язі..
Розглянемо вантаж, підвішений до троса AB /рис. 2.10/. З боку вантажу до троса прикладена сила /сила ваги 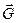 /, яка викликає натяг цього троса. Але на підставі п’ятої аксіоми з боку троса на ватаж повинна діяти така сама за величиною сила
/, яка викликає натяг цього троса. Але на підставі п’ятої аксіоми з боку троса на ватаж повинна діяти така сама за величиною сила 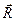 , яка напрямлена в протилежний бік. Силу, з якою в’язь діє на тіло, називають реакцією в’язі, або скорочено реакцією /від латинського re... проти + actio дія, тобто - протидія/.
, яка напрямлена в протилежний бік. Силу, з якою в’язь діє на тіло, називають реакцією в’язі, або скорочено реакцією /від латинського re... проти + actio дія, тобто - протидія/.
Реакції в’язей за своєю природою відрізняються від інших діючих на тіло зовнішніх сил, які можуть викликати рух тіла, і називаються активними силами /наприклад, сили ваги, сили пружності пружини, стиснутого газу, рідини, електричної взаємодії тощо/. Ця різниця полягає в тому, що реакції в’язей не зовсім визначаються самою в’яззю; її модуль, а інколи і напрям, залежить ще від інших /активних/ сил, які діють на тіло. У разі відсутності активних сил реакції взагалі не виникають. Модуль і напрям кожної активної сили, як правило, відомі заздалегідь і від інших прикладених до тіла сил не залежать. Крім цього, активні сили, що діють на тіло, що знаходиться у спокої, можуть надати йому той або інший рух /звідси й термін "активні"/; реакції в’язей цих властивостей не мають, тому на відміну від активних сил їх називають пасивними.
Задачі на рівновагу невільних тіл розв'язуються на основі такого очевидного принципу.
Аксіома в’язей /принцип звільнення/. Будь-яке невільне тіло можна розглядати як вільне, якщо умовно відкинути в’язі й замінити їх дію реакціями.
Користуючись цим принципом, можна застосувати до невільних тіл умову рівноваги, яка встановлена у статиці для вільних тіл. Треба тільки в число сил, що діють на тіло, обов'язково включити і реакції відкинутих в’язей.

Рис. 2.I0
У задачах статики вивчають невільні тіла, які перебувають у стані рівноваги, причому навантаження /активні сили/, що діють на ці тіла, бувають задані, а реакції в’язей необхідно визначити. Знаючи реакції в’язей, згідно з п’ятою аксіомою, знатимемо і сили, які сприймаються в’язями /дія дорівнює протидії/, що необхідні для розрахунку міцності відповідних частин і конструкції машин, споруд і т. ін. Але реакція як сила є векторна величина і характеризується трьома елементами: модулем, напрямом і точкою прикладення. Отже, визначити реакцію в’язі - це означає визначити кожний із цих трьох елементів.
Найпростіше розв'язуються питання про точку прикладання реакції: вона визначається місцем стикання в'язі з тілом.
Модулі реакцій визначаються виходячи з умов рівноваги тіла, умовно звільненого від в'язей. Скористатися цими умовами рівноваги, як правило, стає можливим лише тоді, коли попередньо відомі напрями шуканих реакцій. Тому визначення напряму реакцій при розв'язанні задач статики має виключно важливе значення.
Реакція в’язі завжди напрямлена в бік, протилежний тому, в який дана в’язь перешкоджає переміщенню тіла. Коли в’язь перешкоджає переміщенню тіла по кількох напрямах одночасно, то напрям її реакції завчасно невідомий і повинен визначатися у результаті розв'язання задачі, яка розглядається.
Розрізняють в’язі з тертям і без тертя. Зрозуміло, що останніх у природі не існує. Проте у процесі розв'язання деяких задач механіки силою тертя /порівняно з іншими силами, які діють на тіло/ можна знехтувати. В’язі з тертям називають реальними, без тертя - ідеальними. У курсі теоретичної механіки, як правило, розглядаються ідеальні в'язі.
Розглянемо деякі типи в'язей, що найчастіше зустрічаються, і правила визначення їх реакцій.
Гнучка в'язь.
Прикладами такої в'язі можуть бути нитка, трос, канат, ланцюг, пас тощо, які умовно вважаємо абсолютно невагомими і нерозтяжними, тобто ідеальними /рис. 2.I0, 2.11/. Гнучка в'язь не дає змоги тілу С віддалитися від точки закріплення А у напрямі дії сили 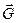 . Тому реакція гнучкої в'язі завжди напрямлена вздовж цієї в’язі від тіла до точки підвішування А.
. Тому реакція гнучкої в'язі завжди напрямлена вздовж цієї в’язі від тіла до точки підвішування А.
2. Гладка опорна поверхня. Гладкою називають поверхню, тертям тіла з якою можна знехтувати. Оскільки гладка обрана поверхня не перешкоджає переміщенню тіла по ній, то реакція 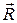 гладкої поверхні /рис. 2.12 а,б/ напрямлена завжди по спільній нормалі до поверхні тіла і поверхні в’язі в їх точці дотику. Нормаллю n-n /рис. 2.І2 в/ до поверхні, називають перпендикуляр до дотичної площини
гладкої поверхні /рис. 2.12 а,б/ напрямлена завжди по спільній нормалі до поверхні тіла і поверхні в’язі в їх точці дотику. Нормаллю n-n /рис. 2.І2 в/ до поверхні, називають перпендикуляр до дотичної площини  поставлений через точку дотику А.
поставлений через точку дотику А.
3. Упор - це опора, утворена двома гранями двогранного кута /рис. 2.13/. Такий вид в'язі перешкоджає переміщенню тіла в двох взаємно перпендикулярних напрямах незалежно від конструкції упора. У цьому випадку виникає дві взаємно
перпендикулярні складові реакції 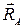 і
і 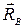 або
або 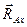 і
і 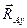 .
.
4. Шарнірно-нерухома опора /нерухомий шарнір/ дає змогу тілу вільно повертатися відносно опори, але перешкоджає його лінійним
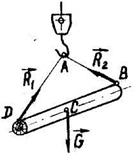 Рис. 2.11
Рис. 2.11
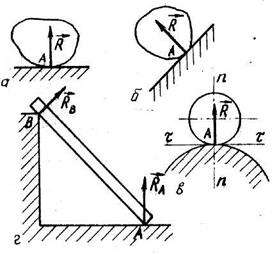
Рис. 2.12
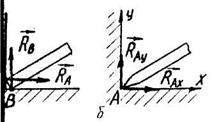
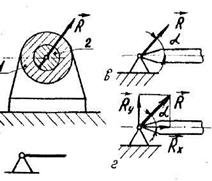 Рис. 2.14
Рис. 2.14
Рис. 2.13
переміщенням у всіх напрямах /рис. 2.14/. Найпростіший шарнір /рис. 2.14,а/ складається з втулки І і пальця 2, тому його ще називають циліндричним шарніром. При складанні палець входить у втулку із зазором, необхідним для забезпечення вільного обертання пальця у втулці, і у випадку, зображеному на рис. 2.14,а, втулка нерухома, а палець зв’язаний з тілом, яке може рухатися. Конструктивне виконання такої опори може бути іншим: палець нерухомий, а втулка рухома. Умовні зображення шарнірно-нерухомої опори наведено на рис. 2.І4,б,в.
Зручно розкласти реакцію опори на дві складові: горизонтальну 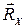 та вертикальну
та вертикальну 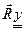
 що відповідає векторному рівнянню:
що відповідає векторному рівнянню: 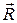 =
= 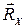 +
+ 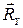 (2.2 )
(2.2 )
У загальному випадку напрями осей можуть бути іншими.
Після того, як будуть знайдені модулі кожної із складових реакцій, за необхідністю можна знайти модуль повної реакції 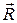 та її напрям, який визначається кутом a.
та її напрям, який визначається кутом a.
5. Шарнірно-рухома опора. Раніше йшлося про в’язі, які створюють абсолютно гладкі поверхні. Ці в’язі перешкоджають переміщенню тіл тільки в напрямі, нормальному до поверхні. Проте сили тертя, які виникають у місцях стикання тіл, ускладнюють їх переміщення по самій поверхні. Для того, щоб зменшити вплив сил тертя на реакції опор, використовують опори на котках /рис. 2.15, а/. Такі опори не перешкоджають переміщенню осі шарніра паралельно опорній площині, а тому їх реакції напрямлені перпендикулярно до опорної площини і проходять через центр шарніра. Умовне зображення шарнірно-рухомої опори показано на рис. 2.15,б. Реакція опори напрямлена завжди по нормалі до опорної поверхні.
6. Підп’ятник/рис. 2.16/ можна уявити як об’єднання циліндричного шарніра
/рис. 2.15,а/ і опорної поверхні. Така опора І дозволяє обертатися валу 2 навколо осі Z і переміщатися вздовж цієї осі, але тільки в одному напрямі.
Реакція підп’ятника складається з реакції циліндричного підшипника /шарніра/, яка лежить у площині хОу /у загальному випадку її можна розкласти на складові 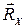 і
і 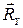 , і нормальної реакції
, і нормальної реакції 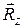 опорної поверхні.
опорної поверхні.
7. Сферичний шарнір /рис. 2.17/. Стержень /вед/ І має на своєму кінці 0 сферичну поверхню, яка розміщена в сферичній опорі 2. Такий шарнір дозволяє обертатися валу навколо будь-якої осі (х, у, z ). Про реакцію сферичного шарніра можна сказати лише те, що вона проходить через точку О
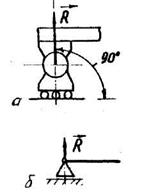 Рис. 2.15
Рис. 2.15
Рис. 2.16 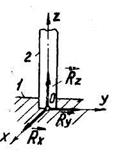
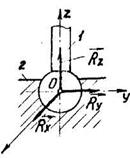
Рис. 2.17
/центр шарніра/, якщо не враховувати сили тертя. Напрям цієї реакції, у просторі може бути довільним , а тому при розв'язанні задач, як і у випадку підп’ятника, повну реакцію можна визначити через три складові, 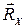 ,
, 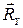 ,
, 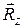 що напрямлені вздовж трьох координатних осей х,у,z.
що напрямлені вздовж трьох координатних осей х,у,z.
Жорстке защемлення
Така в’язь (рис. 2.18) здійснюється вмуровуванням тіла в нерухому поверхню. При цьому обмежується переміщення тіла в площині його розміщення та обертання тіла навколо точки закріплення.
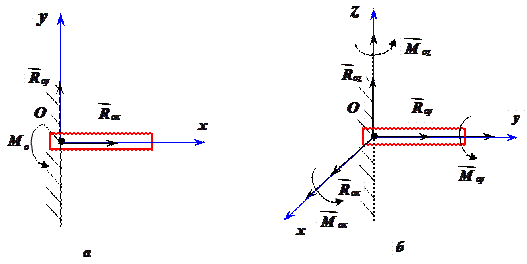
Рис.2.18
Стержньова в’язь.
Часто замість гнучкої в’язі використовують стержні, які приймають абсолютно жорсткими /недеформованими/ і невагомими тілами з шарнірними закріпленнями на кінцях /див. рис. 2.I9/. Якщо стержні виготовлені прямолінійними, то їхні реакції напрямлені вздовж осей цих стержнів. У криволінійних стержнях /рис. 2.19,а/ реакції в’язей напрямлені вздовж прямої, яка проходить через осі кінцевих шарнірів А і В.
Прямолінійні стержні під дією прикладених у шарнірах навантажень можуть працювати на розтяг або стиск. Якщо стержень розтягується, то його реакція напрямлена вздовж стержня від вузла /див. рис. 2.19, а/. Якщо стержень стискається, то його реакція напрямлена до вузла. Вузол - це місце з'єднання стержнів.
На відміну від гнучкої в’язі, яка працює тільки на розтяг, стержневі в’язі можуть працювати на розтяг або на стиск.
Алгебраїчне значення сили, яка діє вздовж осі стержня, називають зусиллям у стержні.
При розв'язанні задач не завжди наперед можна визначити, який із стержнів працює на розтяг, а який на стиск. Тому умовно приймають, що всі стержні працюють на розтяг, а в результаті розв’язання одержують значення реакцій стиснутих стержнів зі знаком "-".
На практиці, як правило, стержні з'єднують наглухо з допомогою заклепок або зварних швів. У такому випадку стержні працюють не тільки на розтяг або стиск, але й на згин. Проте згинальні сили порівняно з осьовими часто бувають невеликими і ними можна знехтувати.
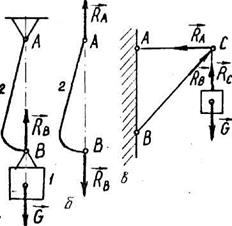
Рис. 2.19
Задачі статики
У розділі статики розв’язують дві основні задачі.
1. Задача про зведення сил, тобто задача про заміну заданої системи сил іншою, зокрема найпростішою, їй еквівалентною.
2. Задача про рівновагу, тобто встановлення умов, яким повинна задовольняти система сил, прикладених до заданого тіла /або матеріальної точки/, щоб вона була зрівноваженою системою.
При розв'язуванні першої задачі всі діючі на тіло сили вважаються відомими. Ця задача має важливе значення не лише в статиці, але й в динаміці. Методи розв'язування таких задач розглядатимуться окремо для кожної системи сил.
Друга задача ставиться тоді, коли наперед відомо, що тіло знаходиться у рівновазі.
Питання для самоконтролю
1. Чим відрізняється матеріальна точка від геометричної?
2. Яке тіло називається абсолютно твердим?
3. Що називається силою, системою сил? Якими елементами визначається сила?
4. Які дві системи сил будуть еквівалентними?
5. Що розуміють під рівновагою тіла, сил?
6. У чому схожість і різниця між рівнодіючою та зрівноважуючою силами; зовнішніми та внутрішніми силами?
7. Сформулюйте аксіоми статики і наслідки з них.
8. Що розуміють під в’язями та їх реакціями ? Чим відрізняються активні сили від реакцій?
9. Назвіть основні види в’язей. Як знаходити їхні реакції?
10. Чи залишаються постійними реакції в’язей при зміні зовнішніх сил, що діють не тіло?
11. Задачі статики.
Заняття № 3
Дата добавления: 2016-01-26; просмотров: 10868;
