Миттєвий центр прискорень

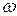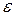Миттєвим центром прискорень (МЦП) плоскої фігури, що рухається непоступально ( і одночасно не дорівнюють нулю), називається така її точка 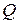, прискорення якої в даний момент часу дорівнює нулю.

Припустимо, що є відомими за модулем і напрямком прискорення будь-якої точки А плоскої фігури, а також кутова швидкість і кутове прискорення цієї фігури. Якщо взяти за полюс точку А, то для точки 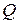прискорення

.

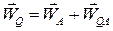Але точка 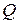– це МЦП і 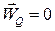, тому

.

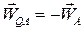Таким чином, вектор прискорення точки 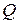в її обертанні навколо полюса А протилежний за напрямком вектору 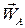, і рівний йому за модулем. Тоді :

,

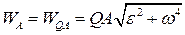(25.5)

звідкіля відстань МЦП від даної точки А

.

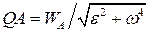(25.6)

Очевидно, що рівняння (2.45) справедливе і для будь-якої іншої точки В плоскої фігури. Тому можна записати, що

.

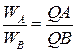(25.7)

Останнє співвідношення означає, що прискорення точок тіла, яке здійснює плоский рух, пропорційні їх відстаням до МЦП. Причому вектори прискорень точок тіла утворюють один і той же кут 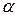з відповідними відрізками, що з’єднують ці точки з МЦП (рис.24.7). Величина кута 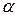визначається формулою:

.

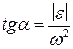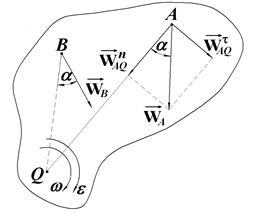
Рис. 24.7