Додавання прискорень в складному русі

Теорема Коріоліса:

Абсолютне прискорення точки дорівнює геометричній сумі трьох прискорень – переносного, відносного і коріолісова (поворотного).

Для визначення абсолютного прискорення точки М (рис.26.2) продиференціюємо за часом рівняння 26.2).

(26.8)

Перший доданок в правій частині отриманого рівняння являє собою прискорення центра О рухомої системи координат відносно нерухомої системи відліку.

Другий доданок є другою похідною від радіуса-вектора 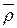, в припущенні, що координати точки М відносно до осей 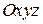сталі. Отже другий доданок – це прискорення відносно центра О рухомої системи відліку тієї її точки, з якою в даний час збігається точка М. Тому перший і другий доданки разом дають прискорення відносно нерухомої системи відліку тієї точки рухомого тригранника, з якою в даний момент збігається точка М. А це і є прискорення переносного руху точки М - .

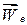Третій доданок відповідає другій похідній від радіуса-вектора 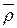в припущенні, що орти рухомої системи відліку сталі величини, напрями яких не змінюються. З цього виходить, що третій доданок визначає прискорення точки М по відношенню до рухомих координат і таким чином є відносним прискоренням .

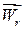З’ясуємо фізичний зміст четвертого доданку рівняння (23.8). За формулою Ейлера вектор лінійної швидкості точки тіла, що обертається з кутовою швидкістю ,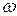

,

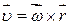де 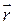- радіус-вектор точки.

Оскільки 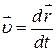, то

.

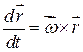Очевидно, що похідні за часом від одиничних векторів рухомої системи відліку також можна розглядати як векторні добутки вектора переносної кутової швидкості на ці орти:

.

З урахуванням отриманих співвідношень четвертий доданок набуває вигляду:

,

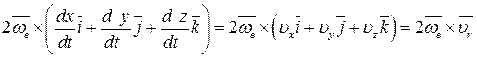де - вектор відносної швидкості точки М.

Кінцевий вираз визначає прискорення Коріоліса, яке позначають через :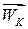

.

(26.9)

Таким чином, абсолютне прискорення точки в її складному русі дається рівнянням:

,

(26.10)

що і потрібно було довести.

Виникнення прискорення Коріоліса має своїм джерелом додаткове обертання у випадку, коли переносний рух не є чисто поступальним. Воно характеризує зміну відносної швидкості точки в переносному русі і зміну переносної швидкості точки у відносному русі. Тому коріолісове прискорення іноді називають поворотним.

Модуль коріолісова прискорення визначають за формулою:

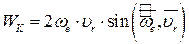
(26.11)

З рівності (26.10) виходить, що коріолісове прискорення дорівнює нулю в таких випадках:

1. 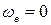, тобто переносний рух є поступальним, або миттєво-поступальним;

2. ( або );

3. .

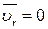Рис.26.5. а

Рис.26.5. б

Напрям коріолісова прискорення визначається за загальним правилом векторного множення: вектор 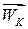напрямлений перпендикулярно до площини, в якій лежать вектори і , в той бік, звідкіля найкоротше суміщення з можна бачити як таке, що відбувається проти руху годинникової стрілки (рис.26.5.а).

Часто для визначення напряму коріолісова прискорення зручно використовувати правило Жуковського, згідно з яким потрібно спроектувати вектор відносної швидкості точки на площину, перпендикулярну до осі переносного обертання (тобто перпендикулярну до вектора ), і отриману проекцію повернути на кут 90⁰ у цій же площині в бік переносного обертання (рис. 26.5.б).

В самому загальному випадку, коли абсолютний, переносний і відносний рухи точки є криволінійними, абсолютне, переносне і відносне прискорення її доцільно подати у вигляді сум нормальних і дотичних складових. Тоді рівняння (26.10) набуває вигляду:

,

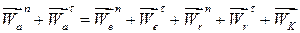(26.12)

При розв’язанні практичних задач кінематики складного руху точки потрібно векторні рівняння (26.10) або (26.12) замінити алгебраїчними, використовуючи метод проекцій.

В прямокутній системі координат 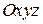у відповідності до рівняння (26.10) отримаємо:

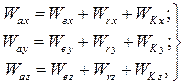
(26.13)

і відповідно з рівнянням (2.59):

.

(26.14)

З наведених алгебраїчних систем рівнянь (26.13) і (26.14) визначають потрібні невідомі.

Питання для самоконтролю

1. Дайте визначення відносного, переносного і абсолютного рухів, а також відповідних швидкостей і прискорень цих рухів.

2. Якою математичною залежністю пов’язані між собою абсолютна, відносна і переносна швидкості?

3. За якою формулою визначається модуль абсолютної швидкості точки при відомих величинах відносної і переносної швидкостей?

4. Як визначається модуль відносної (переносної) швидкості точки при відомих значеннях абсолютної і переносної (відносної) швидкостей?

5. За якою загальною формулою визначається вектор абсолютного прискорення?

6. Які причини появи коріолісова прискорення; як визначити величину і напрям коріолісова прискорення?

7. При яких умовах коріолісове прискорення точки відсутнє?

8. Точка рівномірно рухається вздовж радіуса диска, який, в свою чергу, рівномірно обертається навколо осі, що проходить через центр диска перпендикулярно до його площини. Запишіть в загальному вигляді формулу, за якою визначається модуль коріолісова прискорення. Як залежить величина прискорення Коріоліса від положення точки на диску?

9. Точка рухається по ободу диска, що обертається навколо нерухомої осі, яка проходить через його центр перпендикулярно до площини диска. Чи може одна із складових абсолютного прискорення точки бути напрямленою по радіусу від центра диска? Якщо так, то при яких умовах?

10. Визначити величину і напрям абсолютного прискорення точки, що рухається зі сталою швидкістю 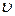вздовж твірної циліндра радіуса 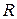, який рівномірно обертається навколо своєї центральної осі з кутовою швидкістю .

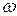Заняття 27

Розділ 3 : Динаміка