Диференціальні рівняння руху матеріальної точки

Як відомо, положення матеріальної точки в інерціальній системі відліку визначається її радіусом-вектором . Сила , що діє на точку, може залежати від положення точки, тобто від радіуса-вектора (наприклад, сила тяжіння), швидкості 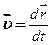точки (наприклад, сила опору) і часу . Отже, в загальному випадку основне диференціальне рівняння (27.1) можна записати в такій формі:

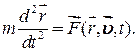
(27.2)

Це рівняння називається диференціальним рівнянням руху матеріальної точки у векторній формі.

Диференціальне рівняння у векторній формі еквівалентне певній системі скалярних (алгебраїчних) рівнянь. В залежності від вибору координатних осей, на які проектується основне рівняння динаміки (27.1), отримують різні форми скалярних диференціальних рівнянь руху матеріальної точки.

Так, якщо спроектувати рівняння (27.2) на координатні осі 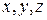декартової нерухомої системи координат, то будемо мати:

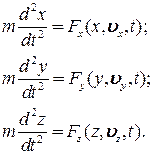
(27.3)

У спрощеній формі запису ця система рівнянь набуває вигляду:

(27.4)

Рис.27.1

При використовуванні природної системи координат для опису руху матеріальної точки потрібно спроектувати основне диференціальне рівняння динаміки (27.2) на осі природного тригранника (рис.27.1); в результаті отримаємо співвідношення:

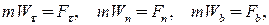
(27.5)

де 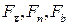- проекції рівнодіючої сил на дотичну, головну нормаль і бінормаль.

Якщо згадати відомі з кінематики вирази для проекцій 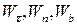повного прискорення точки на ті ж напрями, то отримаємо:

або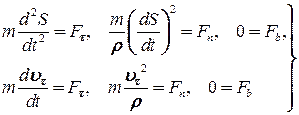

(27.6)

В цих рівняннях 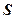- дугова координата (закон руху точки вздовж траєкторії); 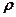- радіус кривизни в поточній точці траєкторії.

Основний закон динаміки і, відповідно, його математичні вирази, наведені вище, сформульовані для вільної матеріальної точки. Якщо на точку накладено певні в’язі, тобто вона є невільною, то на підставі принципу звільнення від в’язей до заданих (активних) сил, що діють на точку, потрібно додати відповідні сили реакції і розглядати матеріальну точку як вільну. Тоді основне рівняння динаміки буде мати вигляд:

,

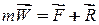(27.7)

а алгебраїчні диференціальні рівняння руху точки в проекціях на осі декартової системи координат і на осі природного тригранника наберуть такої форми:

(27.8)

і

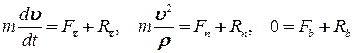
(27.9)

В цих рівняннях 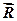- рівнодіюча реакцій в’язей; - складові реакцій в’язей.