Друга (обернена) задача динаміки точки
В задачах такого типу відомі сили, які діють на матеріальну точку, її маса і початкові умови. Останні визначають положення точки і її швидкість в певний момент часу, прийнятий за початковий. Потрібно знайти кінематичні характеристики руху точки (закон руху, швидкість і інколи прискорення).
Розв’язання другої задачі зводиться до інтегрування систем диференціальних рівнянь (27.4) або (27.6) при заданих початкових умовах.
Розглянемо більш детальніше особливості розв’язання другої задачі динаміки точки при умові її прямолінійного руху. Причому координатну вісь х у всіх випадках будемо суміщати з напрямом прямої, вздовж якої відбувається рух. Тоді вектор сили 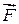 , що діє на точку, повністю визначається його єдиною проекцією
, що діє на точку, повністю визначається його єдиною проекцією 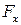 .
.
Виділимо з усієї різноманітності сил такі, що є: а)сталими, б) залежними тільки від часу, в) залежними від положення (координати) точки, г) залежними тільки від швидкості точки.
а. Прямолінійний рух точки під дією сталої сили 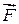 .
.
Диференціальне рівняння в цьому випадку має вигляд:
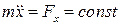
|
звідкіля:
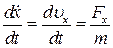 і і 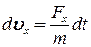 . .
|
Після інтегрування отримаємо:
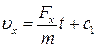 . .
|
Після другого інтегрування з урахуванням того, що 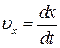 , будемо мати:
, будемо мати:
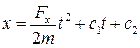 .
.
б. Прямолінійний рух матеріальної точки під дією сили, що залежить тільки від часу.
Вихідне диференціальне рівняння:
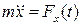
З нього виходить:
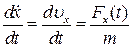 і
і 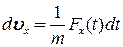 .
.
Після інтегрування отримаємо:
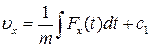 ,
,
а після повторного інтегрування отримаємо:
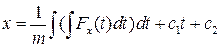 .
.
в. Прямолінійний рух матеріальної точки під дією сили, що залежить тільки від положення точки.
Якщо урахувати, що :
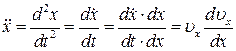 , ,
| (27.10) |
то вихідне диференціальне рівняння руху записується у такій формі:
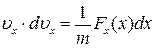 .
.
Після інтегрування знайдемо:
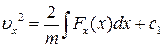 ,
,
звідки:
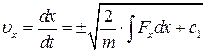 і
і 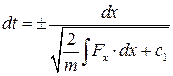 .
.
Повторне інтегрування дає:
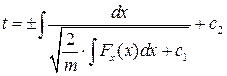 .
.
Тобто 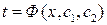 .
.
Розв’яжемо останнє рівняння відносно х і знайдемо закон руху точки в залежності від часу t.
г. Прямолінійний рух точки під дією сили, яка залежить тільки від швидкості цієї точки.
При розв’язанні задачі виникають два варіанти.
Перший варіант. Умова задачі дозволяє визначити швидкість як функцію часу.
Тоді 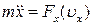 або
або 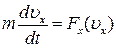 і
і 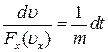 . Після інтегрування отримуємо:
. Після інтегрування отримуємо:
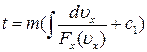 .
.
Якщо з останнього рівняння можна визначити швидкість як функцію від часу, тобто:
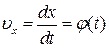 ,
,
то після інтегрування цього виразу маємо:
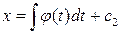 .
.
Другий варіант. При неможливості визначити швидкість як функцію часу, записуємо вихідне диференціальне рівняння у такій формі (дивись пункт «в»):
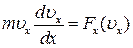 .
.
Тоді 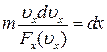 і
і 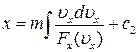 .
.
З останнього співвідношення визначаємо: 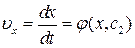 . Ітегруємо і отримуємо:
. Ітегруємо і отримуємо: 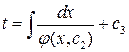 ,
,
звідки визначаємо х як функцію від t.
Питання для самоконтролю
1. Які закони Ньютона лежать в основі динаміки?
2. Наведіть приклади сил, що діють на матеріальну точку, які є: а) сталими; б) залежними від часу; в) залежними від швидкості; г) залежними від положення цієї точки.
3. Напишіть диференціальні рівняння руху матеріальної точки в проекціях на осі нерухомої декартової системи координат і на осі природного тригранника.
4. Яка різниця між диференціальним рівнянням руху вільної і невільної матеріальної точки?
5. У чому полягає суть прямої та оберненої задачі динаміки?
6. Як визначаються сталі інтегрування при розв’язанні диференціальних рівнянь руху точки?
7. Чи достатньо задання сили для визначення конкретного руху точки? Чому?
8. При виконанні яких умов точка буде рухатись під дією сили: а) прямолінійно; б) в одній площині?
9. У випадку дії на точку яких сил диференціальне рівняння прямолінійного руху доцільно брати у вигляді: 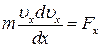 ?
?
10. Які умови потрібно накласти на сили, що діють на матеріальну точку, щоб остання рухалась рівномірно по криволінійній траєкторії?
11. При яких умовах сума проекцій сил, прикладених до точки, на головну нормаль траєкторії дорівнює нулю?
12. Вантаж масою 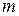 рухається по похилій площині з кутом нахилу
рухається по похилій площині з кутом нахилу 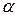 ; коефіцієнт тертя вантажу по площині дорівнює
; коефіцієнт тертя вантажу по площині дорівнює 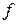 . Чи будуть однаковими диференціальні рівняння руху вантажу по цій площині вверх і униз?
. Чи будуть однаковими диференціальні рівняння руху вантажу по цій площині вверх і униз?
Заняття 28
Тема: Сила інерції.
План
- Сила інерції матеріальної точки.
2. Визначення її напрямків та величини для різних видів руху матеріальної точки.
ЛІТЕРАТУРА ОСНОВНА
ЛІТЕРАТУРА ДОДАТКОВА
Студенти повинні знати: визхначення сили інерції та її використання.
Студенти повинні вміти: визначати величину та напрямок сили інерції при криволінійному та прямолінійному русі.
Дата добавления: 2016-01-26; просмотров: 2188;
