Поняття про сили інерції
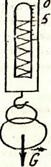
Скориставшись динамометром /пружинною вагою/, зважимо деякий вантаж. Взявши гирю, сила ваги якої 5 Н, підвісимо її до гачка ваги. Покази на шкалі - 5Н /рис. 28.І,а/.
При рівномірному підніманні ваги разом з гирею покази не змінюватимуться.
Коли ж вагу при зважуванні переміщати вгору з прискоренням, то покази будуть уже більшими /рис. 28.І,б/.
|
 Дослідним шляхом можна встановити, що покази ваги збільшуватимуться пропорційно збільшенню прискорення. Зі зменшенням прискорення покази зменшуватимуться, а при
Дослідним шляхом можна встановити, що покази ваги збільшуватимуться пропорційно збільшенню прискорення. Зі зменшенням прискорення покази зменшуватимуться, а при 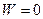 , тобто при рівномірному русі, покази ваги відповідатимуть силі ваги гирі.
, тобто при рівномірному русі, покази ваги відповідатимуть силі ваги гирі.
Сила протидії в боку точки, якій надається прискорення, називається силою інерції.
Сила інерції напрямлена в бік, протилежний напряму прискорення, і прикладена до тіла, що надає прискорення.
| Рис. 28.І |
Силу інерції, зображену на рис. 28.І, позначатимемо 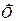 . Прикладена вона до гачка ваги, тобто в"язі, через яку гирі надається прискорення.
. Прикладена вона до гачка ваги, тобто в"язі, через яку гирі надається прискорення.
Сила інерції дорівнює добутку маси матеріальної точки на її прискорення і у векторному вигляді:
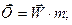 (28.1 )
(28.1 )
Модуль цієї сили можна визначити за формулою:
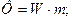 (28.1' )
(28.1' )
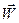 - вектор прискорення;
- вектор прискорення;
де m- маса рухомої точки.
і повсякденному житті ми часто відчуваємо дію сили інерції на собі. Наприклад, при підніманні ліфта з прискоренням /на початку піднімання/ ми відчуваємо появу деякої "важкості" в ногах, і навпаки, на початку опускання відчувається "полегшення". Відчуття ці тим сильніші, чим більші прискорення /сповільнення/ ліфта. Виходячи з виразу /28.І/ можна зробити висновок, що при підніманні ліфта з прискоренням 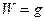 сила інерції дорівнює силі ваги і людина, що піднімається в ліфті, відчуває подвійну силу ваги.
сила інерції дорівнює силі ваги і людина, що піднімається в ліфті, відчуває подвійну силу ваги.
Отже при прямолінійному русі тіла із прискоренням сила інерції направлена вздовж лінії переміщення у бік протилежний прискоренню ( але не руху ).
У загальному випадку змінного криволінійного руху ( швидкість змінюється за величиною та напрямком ) силу інерції можна розкласти на складові дотичну ( чи тангенціальну ) 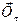 , направлену у бік протилежний напряму дотичного прискорення
, направлену у бік протилежний напряму дотичного прискорення 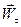 і нормальну
і нормальну
(відцентрову) 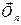 , напрямлену в бік, протилежний нормальному /доцентровому/ прискоренню
, напрямлену в бік, протилежний нормальному /доцентровому/ прискоренню 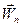 , тобто від центра кривини траєкторії.
, тобто від центра кривини траєкторії.
На рис. 28.2 показано матеріальну точку масою m, що рухається зі змінною швидкістю по криволінійній траєкторії. Коли в розглядуваний момент часу прискорення
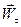
 дорівнюють і
дорівнюють і 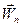 модулі сил інерції точки визначаються з виразів:
модулі сил інерції точки визначаються з виразів:
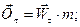 (28.2 )
(28.2 )
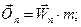 (28.3 )
(28.3 )
| Рис. 28.2 |
Повна сила інерції 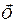 , що збігається з діагоналлю прямокутника, побудованого на
, що збігається з діагоналлю прямокутника, побудованого на 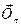 і
і 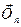 та її модуль можуть бути визначені за формулою
та її модуль можуть бути визначені за формулою
Ф=√(Фt)2+(Фn)2 . 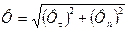 ; (28.4 )
; (28.4 )
Для точки тіла, що здійснює обертальний руx
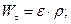
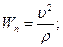
тому сили інерції можуть бути визначені за формулами:
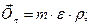 (28.5 )
(28.5 )
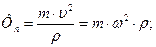 (28.6 )
(28.6 )
Фізично відцентрову силу інерції можна відчути при обертанні тіла M/рис. 28.3/, прив"язаного до нитки. Коли нормальне прискорення 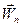 , то на тіло діє доцентрова сила
, то на тіло діє доцентрова сила

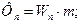
a сам вантаж діє на нитку з відцентровою силою
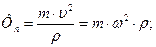
| Рис. 28.З |
Чим більша кутова швидкість нитки з тілом, тим більша Фn і тим сильніше натягується нитка.Очевидно, що можна розвинути таку швидкість обертання, за якої відцентрова сила інерції перевершить за величиною силу опору розриву нитки і тіло обірветься. В момент розриву дія сил Фg і Фn перестане впливати і тіло почне рухатися по дотичній до кола зі швидкістю υ .
На дії відцентрової сили основано виконання "мертвої петлі" на літаку, мотогонки по вертикальній стіні, робота сепараторів для очищення пального й мастил від води і багато інших пристроїв.
Наведені приклади показують, що сили інерції є реальними силами, які активно діють на тіла, розтягують пружину ваги, розривають нитку при обертанні тіла і т.ін.
Про реальний прояв дії сил інерції можна говорити лише при наявності в"язів, через які надається тілу прискорення: при підніманні вантажу з прискоренням натяг нитки більший за силу ваги вантажу на величину сили інерції, під час здійснення "мертвої петлі" сила інерції вдавлює пілота в сидіння.
Сили інерції, що виникають при русі з прискоренням окремих частин машини /поршня, шатуна, колінчастого вала/, викликають в них додаткові напруження, ї, крім того, вони змінюючись за величиною і напрямом, можуть надавати машині ряд періодичних поштовхів, які згубно впливають на фундамент. Щоб запобігти цьому, сили інерції та їхні моменти повинні бути зрівноваженими.
Від розглянутого прикладу /рис. 28.З/ легко перейти до технічного прикладу, уявивши собі замість нитки спицю маховика, в замість тіла М - частину обода маховика. При доборі діаметра маховика необхідно враховувати швидкість, що розвивається на ободі, бо коли вона буде більшою за допустиму, маховик під дією відцентрової сили може розірватися.
Задача 28.І.
Тіло масою 1,5 кг, прив’язане до нитки довжиною l= 0,7 м, обертається у вертикальній площині. Опір розриву нитки Fp= 66 Н. Визначити найменшу кутову швидкість, за якої нитка розірветься.
Розв"язання. Найбільшого значення сила, що діє на нитку, сягатиме в мить, коли тіло проходить нижнє положення по вертикалі, тому що при цьому відцентрова сила інерції 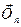 додається до сили ваги
додається до сили ваги 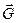 тіла. _
тіла. _
Нитка розірветься при силі натягу Fp=Фn+G , тому сила
інерції в мить розриву повинна бути Фn=Fp-G=Fp-mg=66-1,5·9,81=51,28 Н.
Найменша кутова швидкість, що відповідає одержаному значенню Фn , визначається із формули
Фn= ω2mρ
Де ρ=l , 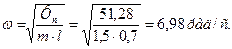
Із формули ω=πn/30 знайдемо частоту обертання /об/хв/, за якої відбувається розрив нитки:
n=(30·ω)/π=(30·6,98)/3,14=67 об/хв.
Питання для самоконтролю:
Питання для самоконтролю
1. Що називають інертністю матеріальної точки ?
2. Що таке сила інерції матеріальної точки ?
3. У чому суть принципу Даламбера для матеріальної точки ?
4. Вказати напрямки сили інерції для прямолінійного та криволінійного рухі
Заняття 29
Тема: Сила інерції.
План
1. Принцип Герлама-Ейлера-Даламбера.
2.Метод кінетостатики та його застосування для розв’язання задач.
ЛІТЕРАТУРА ОСНОВНА
ЛІТЕРАТУРА ДОДАТКОВА
Студенти повинні знати: визхначення сили інерції та її використання.
Студенти повинні вміти: визначати величину та напрямок сили інерції при криволінійному та прямолінійному русі. Застосовувати метод Даламбера для вирішення задач.
Але є багато таких інженерних задач динаміки, розв’язання яких методами ньютонівської механіки потребує дуже великих зусиль, а інколи і взагалі неможливе. В таких випадках користуються методами іншої, так званої аналітичної механіки, в основу яких покладено принципи, відмінні від ньютонівських. Засновником цієї вітки механіки був Лейбниць.
Аналітична механіка являє собою великий, багатий ідеями, розділ механіки. Її положення поширюються на такі області, як теорія відносності і квантова механіка, де закони Галілея-Ньютона не можуть бути застосовані.
Для спрощення, щоб не виходити за межі ньютоновської механіки, будемо розглядати ці принципи як такі, що є наслідками законів класичної механіки з додаванням до них аксіоми про звільнення від в’язей. В той же час потрібно розуміти, що це не теореми, які доводяться за допомогою законів Галілея-Ньютона, а саме принципи. Якщо взяти їх за основу, можна отримати і закони Ньютона, і всю ньютонівську механіку.
Розробниками основних принципів аналітичної механіки були французькі вчені Даламбер (1717-1783) і Лагранж (1736-1813).
Принцип Даламбера
Принцип Даламбера дозволяє приводити всі задачі, які відносяться до руху тіл, до більш простої задачі про рівновагу.
Сучасне трактування принципа Даламбера з використанням поняття сили інерції, яке було уведено в механіку на початку ХІХ століття, є фундаментом важливого метода технічної механіки – метода кінетостатики.
Розглянемо матеріальну точку М масою m, що рухається з деяким прискоренням 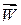 вздовж траєкторії АВ. Припустимо, що на точку діє система активних сил, рівнодіючу яких позначимо через
вздовж траєкторії АВ. Припустимо, що на точку діє система активних сил, рівнодіючу яких позначимо через 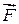 , а також реакції в’язей (у випадку якщо точка є невільною) з рівнодіючою
, а також реакції в’язей (у випадку якщо точка є невільною) з рівнодіючою 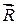 (рис.4.1).
(рис.4.1).
 Тоді, згідно з рівнянням динаміки для невільної точки :
Тоді, згідно з рівнянням динаміки для невільної точки :
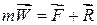 ,
,
або 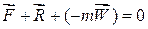 (29.1)
(29.1)
Позначимо:
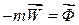 . (29.2)
. (29.2)
Рис 29.1
Вектор 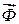 називають даламберовою силою інерції. Її можна розглядати як силу, з якою точка діє на тіла, що надають прискорення даній точці.
називають даламберовою силою інерції. Її можна розглядати як силу, з якою точка діє на тіла, що надають прискорення даній точці.
Сила інерції матеріальної точки за величиною дорівнює добутку маси точки на модуль її прискорення і має напрям, протилежний напряму прискорення (але не руху).
Таким чином, рівність (29.1) набуває вигляду:
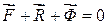 . .
| (29.3) |
Останнє рівняння і виражає принцип Даламбера:
для невільної матеріальної точки в кожний момент часу сума активних сил, що прикладені до точки, реакцій її в’язей і сили інерції дорівнює нулю.
При координатному способі задання руху в системі відліку 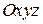 векторне рівняння (29.3) переходить в систему скалярних рівнянь:
векторне рівняння (29.3) переходить в систему скалярних рівнянь:
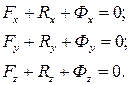
| (29.4) |
Якщо ж рух точки задано натуральним способом, то будемо мати систему таких рівнянь:
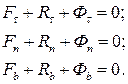
| (29.5) |
В рівняннях (29.4) і (29.5) 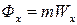 ;
; 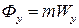 ;
; 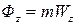 ;
;
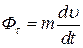 - тангенціальна складова сили інерції;
- тангенціальна складова сили інерції;
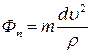 - нормальна (відцентрова) сила інерції;
- нормальна (відцентрова) сила інерції;
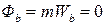 (рис.29.2).
(рис.29.2).
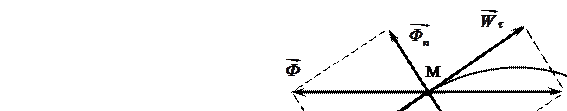
Рис.29.2
Дата добавления: 2016-01-26; просмотров: 4054;
