Робота сили при криволінійному русі.

Розглянемо рух матеріальної точки М під дією сили 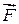вздовж криволінійної траєкторії (рис. 30.3). За нескінченно малий проміжок часу 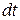радіус-вектор точки 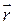отримає приріст 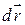, який називають елементарним переміщенням точки .

Рис. 30.3

Скалярний добуток вектора сили 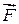на елементарне переміщення точки називають елементарною роботою 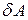сили:

.

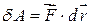(30.4)

Робота сили на будь-якому скінченому переміщенні 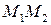точки її прикладання (рис.30.3) визначається як границя інтегральної суми відповідних елементарних робіт:

.

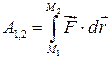(30.5)

В системі СІ одиницею роботи є Джоуль: .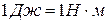

Якщо вектор сили 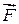і вектор елементарного переміщення 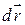точки розкласти по координатних осях:

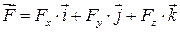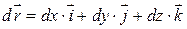, , то отримаємо аналітичні вирази роботи сили:

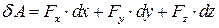.	(30.6)
і 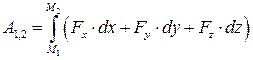.	(30.7)

Останні дві формули визначають роботу сили при координатному способі завдання руху.

Скористаємось співвідношенням для визначення проекції швидкості точки в системі координат 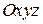: 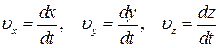, з яких виходить, що 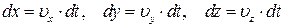. Тоді:

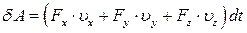,	(30.8)
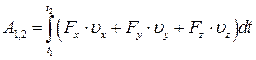.	(30.9)

В натуральній системі координат 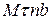елементарне переміщення 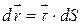, де 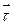-орт дотичної; 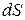- диференціал дуги траєкторії точки, тому елементарна робота сили:

.

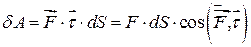(30.10)

Відповідно, повна робота сили:

.

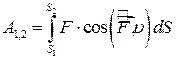(30.11)

В останній формулі 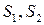- дугові координати, які відповідають положенням 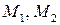матеріальної точки на її траєкторії (рис.30.3).

В інженерній практиці користуються поняттям потужності, якою оцінюють роботу сили за одиницю часу: .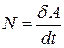

З урахуванням рівняння (30.8), отримаємо:

.

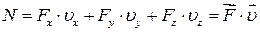(30.12)

Тобто, потужністю сили називається величина, що дорівнює скалярному добутку вектора сили на вектор швидкості точки її прикладання.

Розглянемо приклади обчислення роботи деяких сил.