Перша (пряма) задача динаміки точки
В задачах цієї категорії задані закон руху точки і її маса. Потрібно знайти рівнодіючу сил, яка обумовлює заданий рух. Методика розв’язання полягає у наступному: закон руху підставляють в диференціальне рівняння (27.4) або в (27.6) (в залежності від способу завдання руху) і диференціюванням функцій, якими задано закон руху, визначають проекції шуканої рівнодіючої сил.
Приклад 1
Матеріальна точка масою m рухається в площині 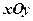 згідно з законом
згідно з законом 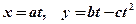 . Знайти силу, під дією якої відбувається цей рух.
. Знайти силу, під дією якої відбувається цей рух.
В даному випадку рух задано в декартових координатах. Тому для розв’язання використовуємо систему рівнянь (27.4). Знаходимо:
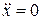 і і 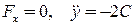 і і 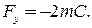
|
Таким чином, з’ясовуємо, що на точку діє стала сила, паралельна осі у і протилежна їй за напрямом.
Приклад 2
Матеріальна точка маси m рухається по колу радіуса r згідно з законом 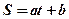 . Визначити силу, під дією якої відбувається такий рух. Закон задано в натуральній формі, тому для розв’язання задачі використовуємо диференціальне рівняння (27.6). Знаходимо:
. Визначити силу, під дією якої відбувається такий рух. Закон задано в натуральній формі, тому для розв’язання задачі використовуємо диференціальне рівняння (27.6). Знаходимо:
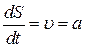 ; ; 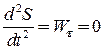 . Тому . Тому 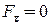 і і 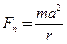 . .
|
Приходимо до висновку, що заданий рух матеріальної точки відбувається під дією сили, сталою за величиною і напрямленою за радіусом кола до його центра.
Дата добавления: 2016-01-26; просмотров: 1072;
