Звідси шляхи можливого спрощення методики додавання похибок зводяться до використання спрощених методів таких переходів.

1.Один із можливих методів ми вже використовували і він базується на тому, що при додаванні великого числа складових, закон розподілу результуючої похибки наближається до нормального. Але таке припущення є ризиковане і використовується при невисоких технологічних вимогах до точності сумарної похибки. Перехід від 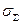до приведеної 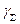виконується за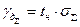
де 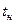- квантільний множник, який визначається по таблицям квантілів нормального розподілу і довірчій ймовірності, або вибирається відповідне значення 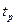квантільного множника Стьюдента при малому числі вимірювань.

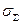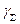2. Другий шлях спрощення переходу від до при визначенні сумарної похибки грунтується на використанні значення довірчої ймовірності 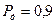, при якій для більшої групи класів різних розподілів зберігається постійним співвідношення 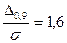. Результуючий розподіл теж належить до цієї ж групи класів і для нього справедливе це ж співвідношення.

Ця унікальна властивість похибки при 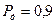відкриває можливість різкого

спрощення методу розрахункового додавання похибок. Так, якщо складові, що додаються, задані своїми значеннями 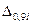, то значення їхніх СКВ 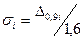; далі використовуємо 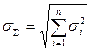, яку знову ж таки переводимо до інтервальної

оцінки 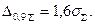Або можемо просто записати: .

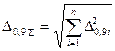3. Використовуючи довірчі межі 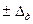(це 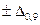або , або 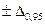...), необхідно врахувати наступне: ці границі довірчої межі розміщуються симетрично тільки тоді, коли в ЗВ чи вимірювального каналу відсутня ССП 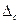. Якщо 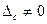, то границі похибки є несиметричними. Наприклад, якщо приведена допустима похибк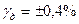а , а 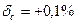то межа одна (нижня) = -0,4 + 0,1 = 0,3%, а друга (верхня) = +0,4 +0,1 = +0,5%. Знак похибки 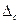частіше за все є невідомим і ввести поправку неможливо. Використовувати такі межі в подальших розрахунках дуже незручно.

Тому, на практиці замість використання несиметричних меж переходить до показу симетричних, рівних по модулю найбільшій межі із несиметричних, тобто, замість запису: „похибка знаходиться в межах від -0,3% до +0,5%” переходять до запису „похибка знаходиться в межах 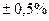”. Імовірність виходу похибки за такі симетричні межі вже в 2 рази менше, так як такий вихід може відбутися практично тільки з однієї сторони, а не з обох. У результаті, якщо 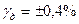була опреділена з 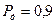, то результуюча 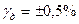є похибкою з довірчою ймовірністю .

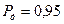Таким чином, якщо 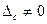, або точніше 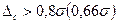то результуюча похибка 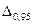легко визначається через модуль ССП 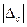та .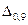

.

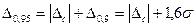Однак подальше спрощення методики додавання похибок, як , наприклад, нехтуванням розділу похибок на сильно та слабо корельовані (в цьому випадку додаються складові, які в дійсності повинні відніматись, тобто, не виконується алгебраїчне додавання ), або нехтуванням розділу похибок на адитивні та мультиплікативні, вже недопустимо і веде до великих помилкових результатів при визначення сумарної похибки інформаційно-вимірювальних систем.

4.Можна використовувати наступніспіввідношення для переходу від СКВ до інтервальної оцінки для інших законів розподілу:

А. Рівномірний закон розподілу: коефіцієнт переходу .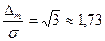

Б. Трикутний закон розподілу (а- основа, 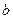- висота трикутнука): .

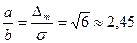В.Трапецієвидний закон розподілу: коефіцієнт переходу залежить від

співвідношення сторін трапеції (а- нижня, в – верхня):

;

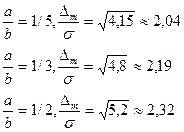Рівномірний закон розподілу мають:

1. похибки квантування в цифрових приладах;

2. похибки при округленні в розрахунках;

3. похибки при відліку показів аналогових приладів;

4. похибки від тертя в приладах з кріпленням рухомої частини на кернах або підп’ятниках;

5. автоматичні мости і потенціометри з слідую чим електромеханічним приводом;

6. похибка визначення моменту часу для кожного із кінців інтервалу часу в електронних вимірювачах частоти.

Коливання напруги живлення змінного струму в енергосистемі постачання підпорядковується приблизно трикутниковому розподілу. Тому якщо відомо, що напруга живлення приладу змінюється в межах 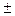5% від номінального 220В, то закон розподілу цієї зміни є трикутним з максимальним відхиленням 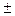11В.