КВАНТІЛЬНА ОЦІНКА ВИПАДКОВОЇ ПОХИБКИ

Площина, яка розміщена, під кривою густини розподілу випадкової величини (або похибки) Р(х), дорівнює 1, тобто, відтворює ймовірність усіх можливих подій. Цю площину розбивають на окремі частини за допомогою вертикальних ліній. Абсциси таких ліній називають квантілі. Так, наприклад, рис.3.9, можна

виділити 2,5%-ну квантіль. Це квантіль, для якої площина під кривою Р(х) зліва від х2 складає 2,5% всієї площини, а справа – залишок, який дорівнює 97,5%.

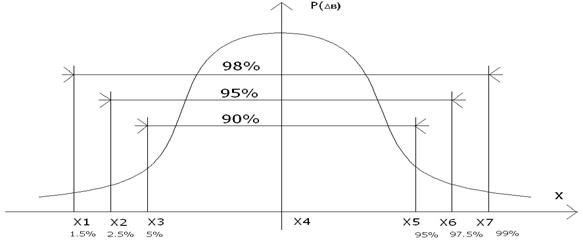
Рис. 3.9. Поняття квантільної оцінки похибки.

По аналогії х6, це 97,5% - на квантіль. Між х2 і х6, тобто, між 2,5%-ною та 97,5%-ною квантілями зосереджено 95% всіх можливих значень похибки, а залишки (5%) – лежать поза її межами. Наприклад, медіана х4 є 50%-на квантіль, так як ділить площину під Р(х) пополам.

Абсциса (х=х1) – є 1.5%-на квантіль, так як площина під кривою зліва складає 1.5% всієї площини. Відповідно квантілі прийнято позначати:

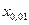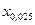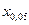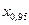як - однопроцентна; - 2,5%; - 5%; - 95%; 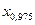- 97,5%.

Інтервал значень х між 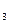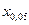х = і х 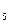= 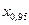охоплює 90% всіх можливих зна

чень похибок і називається інтерквантільним проміжком 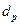з 90%-ною ймовірністю 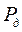=0,9, де ( 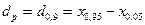) є його протяжність. Відповідно інтерквантільним проміжок: 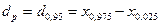охоплює в собі 95% всіх можливих значень похибок (тобто, з ймовірністю 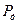=0,95).

У даному випадку х це або випадкова похибка при атестації ЗВ або відхилення вимірюваної величини, від математичного сподівання при її вимірюванні певним ЗВ, тобто випадкова похибка результатів вимірювання.

На основі такого підходу вводиться поняття квантільних оцінок похибки. Квантільна оцінка похибки – це значення похибки 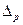як довірчої межі інтервалу невизначеності з заданою довірчою ймовірністю 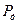. Довірча межа – це верхня та нижня межі інтервалу, у які похибки попадають із заданою ймовірністю. Довірче значення 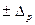випадкової похибки, або її квантільне значення – є її максимальне значення з вказаною довірчою ймовірністю 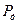і дорівнює половині інтерквантільного проміжку 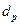, тобто .

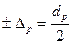У той же час, це є і повідомлення, що частина реалізацій похибки з ймовірністю 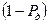може бути і більшою за указане значення похибки. Для позначення встановленого довірчого значення похибки, використовують при позначенні похибки 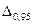індекс (внизу), який чисельно рівний прийнятий довірчій ймовірності. Тобто, замість 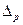(для загального випадку), необхідно писати, наприклад, 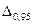(це похибка при довірчій ймовірності ).

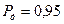Якщо 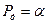є ймовірність 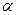, яку вибирають в межах 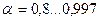, того, що середнє арифметичне відхилення 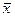(математичне очікування 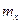) результатів вимірювання відхиляється від істинного значення на величину не більше, ніж випадкова похибка 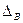, яка дорівнює 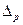або 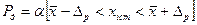, то в цьому випадку 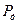називається довірчою ймовірністю, а інтервал від 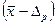до 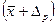називається довірчим інтервалом.

Так як квантілі, які обмежують довірчий інтервал похибки можуть бути вибрані різними, то при повідомленні довірчої мажі оцінки похибки повинно одночасно обов’язково показуватись значення прийнятої довірчої ймовірності 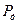. Тобто, для характеристики випадкової складової похибки необхідно задавати два числа :

1. величину самої похибки або довірчим інтервалом

2. довірчу ймовірність .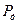

Для переходу при нормальному законі розподілу до квантільної довірчої оцінки похибки 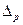з заданою довірчою ймовірністю, використовують визначене значення дослідного СКВ 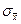та формулу:

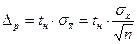(3.37)

де t 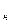- нормована квантіль (коефіцієнт) для заданої ймовірності .

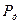Значення квантільного коефіцієнту для нормального закону розподілу:

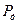
	0,8	0,9	0,95	0,98	0,99	0,995	0,998
t	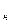1,28	1,64	1,96	2,83	2,58	2,81	3,09

Приведені значення 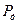і відповідні їм значення 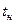нормованої квантілі коректні тільки при нормальному законі розподілу та великій кількості вимірювань n. Між значенням вибраної 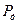(довірчої ймовірності) і необхідною для цього кількістю дослідів (вимірювань) є залежність:

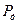
	0,8	0,9	0,95	0,98	0,99	0,995	0,997
N

Як бачимо по дослідним даним легко визначити значення 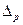тільки з довірчою ймовірністю 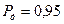(до 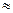80 вимірювань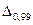), а та 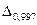практично не реалізуємі (n>400 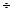1333).

РОЗПОДІЛ СТЬЮДЕНТА

При малому числі n вимірювань (2<n<30) використовування формули для

оцінки 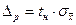є некоректним. Це пов’язане с тим, що формально знайдена для цих випадків оцінка 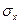(вона позначається для цього випадку через 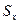у відповідності із співвідношенням 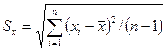) буде мати дуже великий розкид, а знайдена квантільна оцінка розкиду середнього може мати велику похибку. В 1908р. англієць Госсет вивів, і опублікував під псевдонімом „Студент”, залежність коефіцієнта 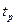(Стьюдента) від кількості вимірювань n та заданою ймовірністю для цих випадків.

Квантілі розподілу Стьюдента для двохстороннього симетричного довірчого інтервалу для кількості вимірювань n та 2-х значень 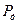має вигляд:

n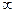
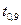
	6,31	2,90	2,35	2,13	1,94	1,83	1,76	1,73	1,70	1,64
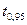
	12,7	4,30	3,18	2,78	2,45	2,26	2,14	2,09	2,04	1,96

Суть використовування цих квантілів в тому, що при n<30 довірче значення похибки оцінки відхилення 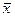(середнього арифметичного) знаходять як:

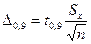(3.38) або 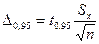(3.39)

Тобто, при зменшенні об’єму даних (n), по якому знаходиться оцінка 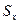для 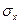, значення 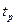Стьюдента різко зростають, але вже при n 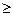8 відмінності квантілів розподілу Стьюдента від нормального розподілу ( 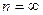) складають вже менше 20%.