ВИЗНАЧЕННЯ СЕРЕДНЬОГО КВАДРАТИЧНОГО ВІДХИЛЕННЯ

Для визначення оцінки дисперсії по результатам дослідних вимірювань замість інтегралу для μ₂ використовують співвідношення:

D_x = 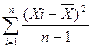, якщо n<20, (3.31)

де Хі – значення окремих вимірювань, 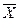- координата центру розподілу; n –

кількість вимірювань ( об’єм вибірки).

Звідси оцінка С.К.В., тобто, розсіювання окремих результатів вимірювання Хі відносно середнього .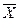

σ_х= 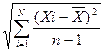(при n<20) (3.32)

Для визначення С.К.В. при кількості вимірювань n≥20 доцільно використовувати:

σ _х= 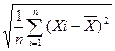(при n≥20). (3.33)

Основним призначенням та перевагою оцінки розсіювання (розкиду) ВП за середнім квадратичним значенням σ_х або дисперсією є можливість визначення дисперсії суми статистично незалежних величин як суми дисперсій складових, не дивлячись на можливі різні закони закону розподілу кожної із величин, що додаються, і не враховуючи можливу деформацію законів розподілу при утворенні композиції. D 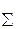= 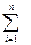D .

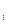Використання С.К.В. σ_х і його квадрату σ_х² = D_x, яке дорівнює дисперсії,

дає можливість:

· Розрахунковим шляхом складати будь-яке число незалежних складових

похибки ЗВ і отримати сумарну похибку ЗВ. Для цього окремі складові похибки ЗВ потрібно попередньо надати своїми середніми квадратичними значеннями σ_х та провести геометричне додавання (геометричне додавання – це додавання через корінь квадратний із суми квадратів складових):

σ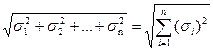_∑= (3.34)

· достатньо точно вирахувати похибку при проектуванні або ЗВ, або інформаційно-вимірювального каналу (ІВК) з наперед заданою сумарною похибкою, використовуючи значення нормованих похибок усіх пристроїв, які складають ЗВ або інформаційно-вимірювальний канал.