ОСНОВНИЙ ЗАКОН ТЕОРІЇ ПОХИБОК

Якщо в одній серії з n вимірювань 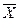_ср є лінійною функцією результатів окремих вимірювань Х1,Х2,..,Хі, і якщо провести нову серію із n вимірювань, то в внаслідок впливу випадкових причин значення Хі будуть відрізнятися від отриманих в першій серії, тобто, нове значення 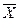буде іншим.

Таким чином, число 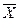, яке отримане в одній із серій вимірювань, є випад-

ковим приближенням до істинного значення Q, необхідно знову ж таки визначити середнє квадратичне відхилення для .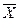

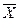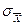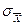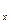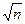Для оцінки можливих відхилень величини від істинного значення, визначають дослідне середнє квадратичне відхилення або середнє квадратичне відхилення середнього арифметичного. Значення дослідного СКВ зменшуюється, порівняно з СКВ вихідних результатів вимірювань σ , в раз і дорівнює:

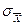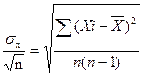= . (3.35)

Ця формула 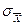= 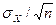- відображає основний закон теорії похибок,суть якого в тому,що якщо потрібно підвищити точність результату вимірювання (при скоригованій систематичній складовій похибки) в n раз, то число вимірювань необхідно збільшити в n 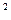раз. Наприклад, якщо потрібно збільшити точність в 3 рази, то число вимірювань n збільшують в 9 раз і т. д.

Таким чином, дослідне СКВ 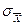оцінює можливі відхилення середнього арифметичного 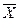результатів вимірювання від істинного (дійсного) значення і використовується для приведення кінцевого результату вимірювань ФВ.

Розподілення похибки статистично визначеного середнього результату багаторазових вимірювань має вигляд, що приведений на рис. 3.7. Якщо б шукане число Хі визначалося шляхом тільки одного вимірювання n =1, то значення Хі випадковим чином може зайняти будь-яке положення в середині смуги похибок. При проведенні n вимірювань для кожного t_i самі результати по-старому будуть розміщуватись випадковим чином у середині тієї ж смуги, але лінія їхніх центрів буде тільки стійкою. Оцінки розсіювання σ_Х та 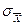необхідно слід чітко відрізняти і пам’ятати, що вони характеризують тільки випадкову складову похибки.

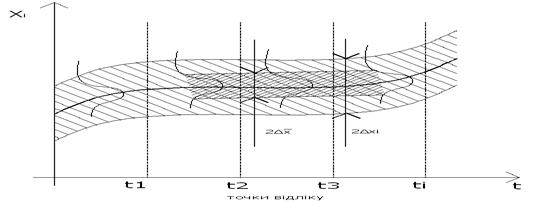
Рис.3.7. Розподілення похибки статистично визначеного середнього

результату багаторазових вимірювань.

Оцінка σ_Хсереднього квадратичного відхилення (СКВ) характеризує ширину смуги невизначеності самих вихідних даних, яка на рис.3.7 зображена широкою смугою (межею) абсолютної похибки 2 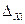. Оцінка ж 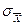(середнього квадратичного відхилення середнього арифметичного) характеризує в 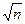раз більш вузьку смугу невизначеності знайдених середніх значень, яка на рис.3.7 зображена вузькою смугою абсолютної похибки 2 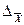. На рис.3.7 середня (жирна) лінія – це значення математичного сподівання M[X] в точці відліку по характеристиці перетворення.

При великому числі n вимірювань систематична складова похибки за

лишається без зміни, а ширина розкиду випадкової складової похибки

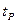
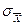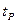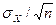= ( )зменшується в 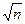раз. Якщо 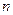достатньо велике, то 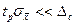і результуюча похибка середнього результату визначається практично тільки його систематичною похибкою.

Стандарт по метрології регламентує, що у випадках, коли ССП 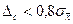, то систематичною складовою похибки можна нехтувати і враховувати тільки випадкову похибку визначеного середнього результату в вигляді .

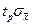Якщо ж 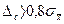, то навпаки, необхідно нехтувати випадковою складовою, а визначений середній результат характеризувати тільки його систематичною похибкою .

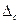Остання умова показує, що наявність невиявленої і не усуненої систематичної похибки робить практично безглуздим використання статистичного визначення середнього.