МАТЕМАТИЧНЕ СПОДIВАННЯ ТА ЙОГО СУТЬ
Математичне сподівання (його ще називають середнім значенням ВП) є основною числовою характеристикою, яка дає координату положення випадкової величини (похибки) на осі чисел, біля якої групуються всі можливі значення ВП (ВВ). Для безперервної величини Х математичне сподівання M[X] дорівнює: M[X] = 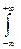 xP(x)dx,(3.25)
xP(x)dx,(3.25)
де P(x) - густина розподiлу величини Х.
Математичним сподіванням випадкової величини (похибки) називається сума добутків усіх можливих значень ВВ (ВП) на ймовірності цих значень.
При дискретних вiдлiках Хi, які мають місце за багаторазових вимірюваннях, обчислення інтегралу замінюється, при великій кількості n реальних вимірювань, еквівалентним вирахуванням середнього арифметичного 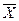 (Хср) : Хср =
(Хср) : Хср = 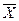 =
= 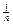

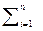 Хi.
Хi.
Таким чином, можна записати, що при n 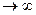 :
:
M[X] = m 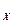 =
= 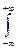 xP(x)dx
xP(x)dx 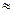
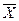 =
= 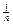
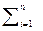 Хi.(3.26)
Хi.(3.26)
Ця формула описує зв'язок мiж математичним сподіванням M[X] випадкової
величини та середнiм арифметичним 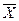 при великій кiлькостi проведених дослiдiв (вимiрювань) і стверджує: «при великiй кiлькостi дослiдiв, середнє арифметичне цих дослiдiв над ВВ (ВП) наближається, або кажуть сходиться по ймовiрностi, до математичного її сподівання». Тому при практичних вимiрюваннях математичне сподівання M[X] i замінюють на середнє арифметичне
при великій кiлькостi проведених дослiдiв (вимiрювань) і стверджує: «при великiй кiлькостi дослiдiв, середнє арифметичне цих дослiдiв над ВВ (ВП) наближається, або кажуть сходиться по ймовiрностi, до математичного її сподівання». Тому при практичних вимiрюваннях математичне сподівання M[X] i замінюють на середнє арифметичне 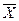 .
.
У механічній інтерпретація математичне сподівання M[X] є не що інше, як абсциса центру вагиданої системи матеріальних точок, відносно якої, провертаючи момент = 0. Цю абсцису, як синонім, ще називають центром розподілу або координатою центру розподілу.
Суть математичного сподівання M[X], тобто, суть пошуку середніх багаторазових вимірювань, у тому, що визначена середня оцінка координати їх центра розподілу має найменшу випадкову похибку, ніж окремі результати вимірювань, по яким вона визначається.
M[X] - є основною числовою характеристикою, яка використовується при статистичному опрацюванні результатів вимірювань.
По-перше, m 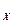 , при метрологічній атестації засобів вимірювання вказує на наявнiсть чи нi систематичної складової похибки (ССП) та дає можливість зробити чіткіше визначення систематичної та випадкової (ВСП) складових похибок:
, при метрологічній атестації засобів вимірювання вказує на наявнiсть чи нi систематичної складової похибки (ССП) та дає можливість зробити чіткіше визначення систематичної та випадкової (ВСП) складових похибок:
ССП - це рiзниця мiж математичним сподіванням результатiв спостережень та iстинним значенням вимірюваної величини:
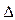 c = M[X] - Q
c = M[X] - Q  .
.
ВСП - це рiзниця мiж результатом одиночного спостереження i математичним сподіванням результатiв спостережень:
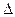 в = Xi - M[X].
в = Xi - M[X].
По-друге, у теорії опрацювання результатів прямих вимірювань, коли необхідно отримати достовірну інформацію про значення вимірюваного параметру за допомогою певного засобу вимірювань, за найбільш ймовірне значення вимірюваної величини Хі необхідно прийняти математичне сподівання M[X] із ряду вимірювань, при якому сума квадратів абсолютних похибок (мінімальна) найменша.
При дискретних відліках і при достатньо великому числі n вимірювань, до дійсного (істинного) значення вимірюваної величини наближається середнє арифметичне 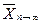 . Виходячи із цього можна вивести, при відсутності в ЗВ систематичної складової похибки (або при нехтуванню нею, або при її врахуванні відповідною поправкою):
. Виходячи із цього можна вивести, при відсутності в ЗВ систематичної складової похибки (або при нехтуванню нею, або при її врахуванні відповідною поправкою):
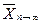 = M[X]
= M[X] 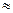 Q
Q  = Q
= Q 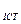 .
.
З іншого боку, при кінцевому значенні числа n вимірювань і не скоригованій ССП:  Q
Q  = M[X] ±
= M[X] ± 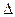 c ±
c ± 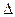 в .
в .
Дата добавления: 2016-01-18; просмотров: 856;
