ДИФЕРЕНЦIЙНИЙ ЗАКОН РОЗПОДIЛУ

Для більш наочного опису результатів вимірювання та випадкових похибок використовують, для безперервних випадкових величин, похідну від функції інтегрального розподілу F(x).

Якщо є безперервна (3.22) випадкова величина Х із функцією розподілу F(x), то можемо вирахувати ймовірність Р попадання цієї ВВ Х на відрізку від х до х+ 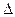х:

P( x < X < x + 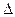x) = F ( x + 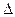x) - F(x),

тобто, імовірність дорівнює приросту функції розподілу F(x) на цьому відрізку.

Тепер розглянемо відношення цієї ймовірності до довжини відрізку, тобто, розглянемо середню ймовірність, яка приходиться на одиницю довжини цього відрізку та будемо наближати 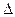x до 0. У крайній межі дістанемо похідну F' від функції інтегрального розподiлу:

lim 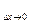{[ F(x+ 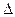x) - F(x)] / 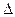x} = F'(x) = P(x). (3.23)

Введене позначенняфункції P(x) – похідної від функції розподілу F(x) характеризує густину, з якою розподіляється значення випадкової величини Х в даній точці.

Функція P(x) називається густиною розподілу, або по іншому: "густиною ймовірності" безперервної випадкової величини Х, або диференціальною функцією розподілу, або диференціальним законом розподілу.

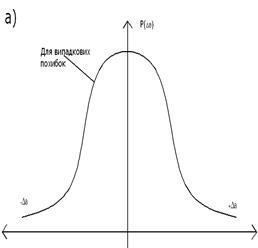
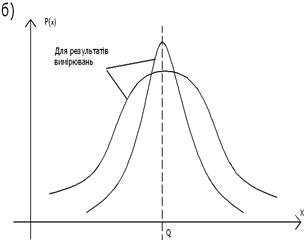
Рис.3.4. Крива розподілу Р(х) дляВСП - а) та РВ - б).

Густина розподілу Р(х), по аналогії з функцiєю розподiлу F(x), є ще

одною із форм закону розподiлу. У протилежність функції розподілу F(x) ця форма Р(x) не є універсальною, так як існує тільки для безперервних випадкових величин.

Графік, який відтворює густину розподілу Р(х) випадкової величини,

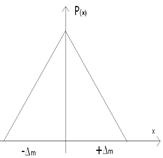
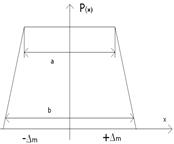
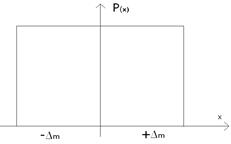
називається кривою розподілу,яка може бути як для випадкової складової похибки ВСП (рис. 3.4,а), так і для результатів вимірювання РВ (рис. 3.4,б). Криві розподілу мають різний вигляд (основні показані на рис. 3.5: трикутний, трапецієвидний, рівномірний і інші), який залежить від кількості впливаючих на подію ( щоб вона відбулася чи ні) факторів та вiд значення цих факторів.

а) б) в)

Рис. 3.5. Криві розподілу: трикутного - а), трапецієвидного - б) та

рівномірного – в) законів.

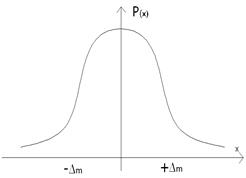
У більшості криві розподiлу мають форму, яка близька до дзвоноподiбної

(рис. 3.6) і відповідають нормальному закону розподілу.

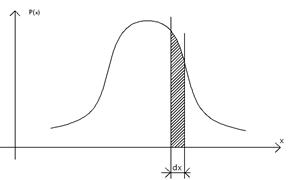а) б)

Рис. 3.6. Крива розподілу нормального закону (а) та елемент ймовірності (б).

Якщо розглянути безперервну випадкову величину Х із густиною розподілення Р(х) та елементарний відрізок dx, який прилягає до точки х, то ймовірність попадання випадкової величини Х на цю елементарну ділянку, з точністю до безмежних малих вищого порядку, дорівнює Р(x)dx i цю величину називають елементом імовірності. Геометрично - це площина елементарного прямокутника, який опирається на відрізок dx (рис. 3.6,б).

Використовування елементів імовірності дає можливість сказати про те, які інтервали значень випадкових похибок більш чи менш імовірні. Наприклад, при дзвоноподібний кривій розподілу Р(x) для випадкових похибок Δв більш ймовірні малі значення похибок, якi лежать навколо випадкової похибки із значенням Δв = 0. Можемо виразити ймовірність попадання випадкової величини Х на відрізок вiд "а" до "в" через густину розподілу. Очевидно, що вона буде дорівнювати сумі елементів імовірності на всьому відрізку, тобто, інтегралу: P("а" <X < "в") = 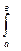Р(x) dx.(3.24)

Геометрична ймовірність попадання величини Х дорівнює площині кривої розподілу, яка опирається на цей відрізок.

Ми можемо вирішити й обернену задачу - виразити функцію розподілу F(x)через густину розподілуР(x). Так як по визначенню F(x) = P(X<x) = P(- < X < x), то використовуючи інтегральну формулу визначення густини розподілу, отримуємо:F(x) = 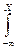Р(x)dx.

Геометрично ймовірність F(x) є, не що інше, як площина під кривою розподілу Р(x), яка лежить лівіше тачки х.

Розмірностіосновних характеристик випадкової величини: 1. Функція інтегрального розподілу F(x), як усяка ймовірність є величиною без розміру. 2. Розмірність густини розподілу P(x) - є обернена розмірності випадкової величини.