Абсолютна і відносна похибки
ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК
Задачі обчислювальної математики
Розв‘язання задач з використанням методів обчислювальної математики потребує виконання великого обсягу обчислювальних робіт, які можна здійснити за допомогою сучасних ЕОМ. При цьому слід уміти оцінити похибку обчисленого розв‘язку, яка містить:
– похибку математичної моделі (модель описує явище наближено, з припущеннями і спрощеннями);
– неусувну похибку, яка зумовлена похибками у вхідних даних (що отримані, наприклад, за допомогою вимірювань);
– похибки методу (пов‘язані з необхідністю заміни неперервної моделі дискретною або з обривом нескінченного ітераційного процесу після скінченної кількості ітерацій);
– обчислювальні похибки (похибки заокруглення чисел, похибки математичних дій та функцій).
Оцінка похибки може бути здійснена за допомогою:
– абсолютної похибки;
– відносної похибки;
– залишкового члену;
– статистичних оцінок.
Абсолютна і відносна похибки
Наближеним числом а є число, яке незначно відрізняється від точного числа А і замінює його при проведенні обчислень.
 Абсолютна похибка наближеного числа а
Абсолютна похибка наближеного числа а
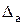 = |А - а|. (1.1)
= |А - а|. (1.1)
Можливі два випадки:
1) точне число А відоме – тоді абсолютна похибка Δа розраховується за формулою (1.1);
2) точне число А невідоме – в такому разі використовують поняття граничної абсолютної похибки
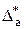 ≥ |А - а|. (1.2)
≥ |А - а|. (1.2)
Значення числа А записують так:
 А = а ±
А = а ± 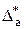
Дата добавления: 2016-02-02; просмотров: 1310;
