Значуща цифра числа. Вірна значуща цифра
Будь-яке наближене число а в десятинній (як і у будь-якій позиційній) системі числення можна записати у вигляді
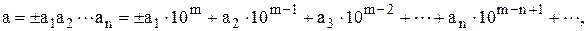(1.5)
де аі – цифри числа (і = 1, 2, …, n) (а1 ¹ 0); m – ціле число (старший розряд числа а).
Приклад 1.3141,59 = 3·103 + 1·102 + 4·101 + 1·100 + 5·10-1 + 9·10-2.
Точність обчислення визначає не кількість десятинних знаків, а кількість значущих цифр результату.
Значущими цифрами числа а називають всі цифри в його десятинному зображенні, починаючи з першої цифри зліва, відмінної від нуля. Наприклад, числа 0,001405 і 5,0300 мають відповідно чотири і п‘ять значущих цифр.
Нулі в кінці числа 5,0300 показують, що число задане з точністю до десятитисячних, інакше вони не були б записані.
Точність наближеного числа залежить не від кількості значущих цифр, а від того, скільки значущих цифр заслуговують довіри, тобто від кількості правильних значущих цифр.
Значущу цифру аn числа (1.5) називають правильною, якщо абсолютна похибка цього числа
Δа £ w·10m-n+1. (1.6)
В залежності від величини w в (1.6) говорять про правильність значущих цифр у вузькому (w = 0,5) і широкому (w = 1,0) сенсі. Якщо нерівність (1.6) не виконується, то цифру аn називають сумнівною. 
Таким чином, приблизне число амістить n правильних цифр (в вузькому сенсі), якщо абсолютна похибка цього числа не перевищує половини одиниці десятинного розряду, який виражається значущою цифрою, рахуючи зліва направо.
Приклад 2. Для точного числа А=17,976 число а=17,98 є приблизним числом з 4-ма вірними знаками в вузькому сенсі, тому що
Δа =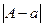 
= 
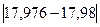= 0,004 ≤ 0,5·101-4+1 = 0,5·10-2 = 0,005.
Число а=17,97 є приблизним з 4-ма вірними цифрами в широкому сенсі, тому що
Δа = =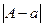 
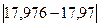= 0,006 < 1·101-4+1 = 1·10-2 = 0,01.
Число а=17,97 є приблизним тільки з 3-ма вірними цифрами в вузькому сенсі, тому що
Δа = 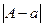= = 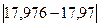0,006 > 0,5·101-4+1 = 1·10-2 = 0,005.
Приклад 3. Визначити скільки вірних значущих цифр містить приблизне число а=85,267 ± 0,0084 в вузькому і широкому сенсі.
Із умови видно, що 0,0084 < 0,05. Тоді в вузькому сенсі:
0,05 = 0,5∙10m-n+1
при m = 1 (розряд десяток) маємо 0,5·10-1 = 0,5∙101-n+1 → -1=1- n +1 → n = 3.
Таким чином, вірними є цифри 8, 5 і 2.
В широкому сенсі 0,0084 < 0,01. При m = 1 (розряд десяток) маємо 1·10-2 = 1∙101-n+1 → -2=1- n +1 → n = 4. Таким чином, вірними є цифри 8, 5, 2 і 6.
Приклад 4.Визначити граничну абсолютну похибку приблизних чисел а=96,387 і b=9,32, якщо вони містять тільки вірні цифри в вузькому і широкому сенсах відповідно.
Тому що для числа а=96,387 остання цифра 7, що стоїтьв розряді тисячних знаків є вірною значущою цифрою в вузькому сенсі, то Δа ≤ 0,5∙0,001, тобто Δ*а = 0,0005. Тоді число а можна записати в вигляді а=96,387 ± 0,0005.
Для числа b=9,32 остання цифра 2, що стоїтьв розряді ситих знаків є вірною значущою цифрою в широкому сенсі, то Δb ≤ 1∙0,01, тобто Δ*b = 0,01. Тоді число b можна записати в вигляді а=9,32 ± 0,01.
1.4 Оцінка похибки функції (Загальна задача теорії похибок)
Задача полягає у визначенні похибки функції U = f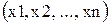 
за відомими абсолютними (граничними) похибками аргументів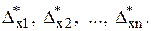 
Розв‘язання загальної задачі одержують за допомогою формул:
= 
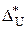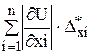; (1.7)
= 
= 
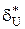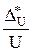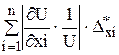. (1.8)
Приклад 5. Визначити граничні абсолютну і відносну похибки об‘єму кулі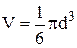 
при 
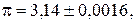
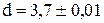см.
В даній задачі аргументами є і d і π, тому що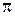 
– теж наближене число. За формулою (1.7) маємо граничну абсолютну похибку
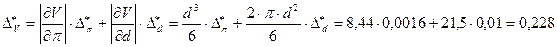см3.
Гранична відносна похибка
.
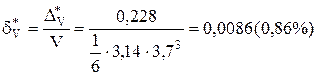Дата добавления: 2016-02-02; просмотров: 2510;