Обернена задача теорії похибок

Задача полягає у визначенні абсолютних похибок аргументів функції, при яких абсолютна похибка функції не буде перевищувати заданого значення. Така задача однозначно розв‘язується тільки для функції одного аргументу. У загальному випадку для її розв‘язання використовують припущення про однаковий вклад всіх доданків у формулі (1.7) на формування похибки функції Δ_U, тобто приймають

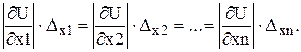
В такому разі із (1.7) маємо

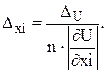(1.15)

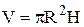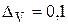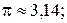
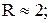
Приклад 7.Розрахунок абсолютних похибок аргументів функції , якщо (при 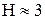) виглядає так

;

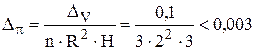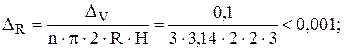
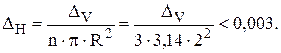
Лекція 2. НАБЛИЖЕНІ МЕТОДИ РОЗВ‘ЯЗУВАННЯ НЕЛІНІЙНИХ

АЛГЕБРИЧНИХ І ТРАНСЦЕНДЕНТНИХ) РІВНЯНЬ

Загальні відомості

Нехай задано рівняння з однією змінною

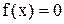, (2.1)

де функція 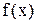визначена і неперервна на деякому проміжку [R_Н, R_В].

Розв‘язати рівняння означає знайти множину його коренів, тобто таких значень 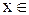[R_Н, R_В], при яких рівняння (2.1) перетвориться в тотожність. Якщо функція 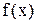– алгебричний багаточлен, то рівняння (2.1) називають алгебричним. Якщо 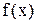містить тригонометричні, показникові або логарифмічні функції, тоді рівняння (2.1) називають трансцендентним.

Універсальних методів для знаходження точних значень коренів алгебричних рівнянь ступеня 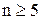і трансцендентних рівнянь не існує. Тому важливого значення набувають наближені методи знаходження коренів рівняння з достатньою для практики точністю.

Задача знаходження коренів рівняння (2.1) вважається розв‘язаною, якщо корені обчислені із наперед заданою точністю.

Наближене знаходження коренів рівняння (2.1) складається з двох етапів:

1) відокремлення коренів, тобто виділення проміжків скінченої довжини (відрізків ізоляції коренів) де міститься один єдиний корінь рівняння;

2) обчислення коренів з наперед заданою точністю (уточнення коренів).

Корені рівняння (2.1) можуть бути дійсними і комплексними. Далі розглянуто наближені методи обчислення тільки дійсних коренів.