Лекція 4. МЕТОДИ РОЗВ‘ЯЗУВАННЯ СИСТЕМ НЕЛІНІЙНИХ РІВНЯНЬ
Метод ітерацій
На відміну від систем лінійних рівнянь не існує прямих методів розв‘язання систем нелінійних рівнянь (СНР) загального виду. Для наближеного їх розв‘язання використовують ітераційні методи. Найбільш поширеними з них є метод ітерацій іметод Ньютона.
Метод ітерацій для СНР по суті є узагальненням методу ітерацій для одного рівняння.
Нехай для обчислення невідомих х1, х2, …, хn необхідно розв‘язати систему
n нелінійних рівнянь
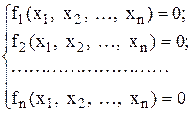 (4.1)
(4.1)
Зобразимо систему (4.1) у вигляді
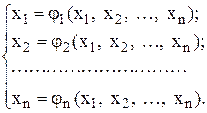 (4.2)
(4.2)
Функції 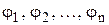 в (4.2) поблизу шуканого розв‘язку мають задовольняти умові збіжності методу ітерацій, яка записується наступнім чином
в (4.2) поблизу шуканого розв‘язку мають задовольняти умові збіжності методу ітерацій, яка записується наступнім чином
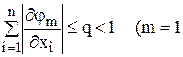 , або 2, …, або n) (4.3)
, або 2, …, або n) (4.3)
(фактично узагальнена умова для одного рівняння).
Задаються початковим наближенням 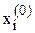 , і = 1, 2, …, n.
, і = 1, 2, …, n.
Взагалі, необхідно, щоб початкове наближення було достатньо близько до шуканого розв‘язку. Вибір наближення провадиться в залежності від конкретних умов, наприклад, з фізичних міркувань. Якщо розв‘язується система із двох рівнянь, то за 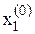 ,
, 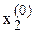 можна прийняти координати точки перетину кривих
можна прийняти координати точки перетину кривих 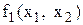 і
і 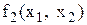 на площині
на площині 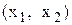 .
.
Наступні наближення визначають за ітераційними формулами

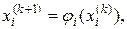 k = 0, 1, 2, … (4.4)
k = 0, 1, 2, … (4.4)
Ітераційний процес завершується при виконанні умови
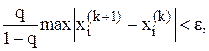 (4.5)
(4.5)
де ε – задана абсолютна похибка розв‘язку.
Одним із суттєвих недоліків методу ітерацій є складність вибору функцій 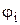 такими, що задовольняють достатній умові збіжності ітераційного процесу. Для системи із двох рівнянь можна рекомендувати наступний засіб (А).
такими, що задовольняють достатній умові збіжності ітераційного процесу. Для системи із двох рівнянь можна рекомендувати наступний засіб (А).
Записують 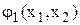 і
і 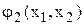 у вигляді
у вигляді
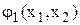
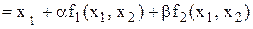 ;
;
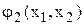
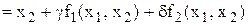 ,
,
де 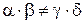 .
.
Коефіцієнти 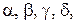 визначають із умов:
визначають із умов:
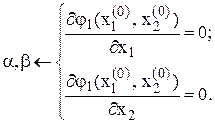
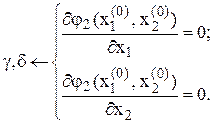 (4.6)
(4.6)
Умова збіжності при цьому виконується, якщо 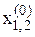 прийняті достатньо близько до шуканого розв‘язку.
прийняті достатньо близько до шуканого розв‘язку.
Для СНР, як і для СЛАР, можливе застосування удосконалення Зейделя, тобто використання раніше визначених невідомих при обчисленні наступних. Власне, для СНР методом ітерацій і називають метод Зейделя.
Метод Ньютона
Цей метод має набагато швидкішу збіжність, чим метод ітерацій.
В основі методу Ньютона для СНР лежить використання розкладення функції 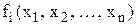 в ряд Тейлора і відкидання членів, що містять похідні порядку вище першого, тобто із рівнянь виділяють лінійні частини, які є головними при малих прирощеннях аргументів.
в ряд Тейлора і відкидання членів, що містять похідні порядку вище першого, тобто із рівнянь виділяють лінійні частини, які є головними при малих прирощеннях аргументів.
Розв‘язання СНР можна записати у вигляді

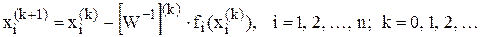 , (4.7)
, (4.7)
де 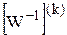 – обернена матриця Якобі
– обернена матриця Якобі
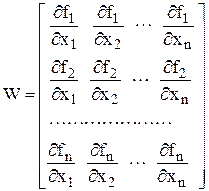 .
.
Для існування єдиного розв‘язку СНР визначник матриці W (його називають якобіаном) не має дорівнювати нулю на кожній ітерації.
Частинні похідні в W можна замінити їх наближеними кінцево-різничними значеннями
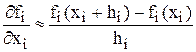 ,
,
де hi – мале прирощення хі, наприклад, 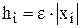 .
.
Ітерації завершуються, коли всі прирощення стають малими за величиною
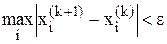 .
.
В методі Ньютона початкове наближення параметрів обирається так же, як і в методі ітерацій для забезпечення збіжності ітераційного процесу.
 Для системи двох нелінійних рівнянь, де прийняті такі позначення: х1 = х і х2 = у,
Для системи двох нелінійних рівнянь, де прийняті такі позначення: х1 = х і х2 = у,
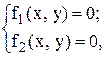 (4.8)
(4.8)
ітераційні формули методу Ньютона в компактній формі мають вигляд:

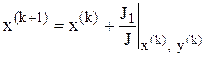 ,
, 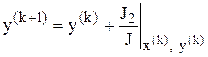 , (4.9)
, (4.9)
де визначники J, J1, J2 являють собою
, , .
Дата добавления: 2016-02-02; просмотров: 2426;
