Апроксимація функцій
Якщо функція 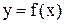 задана таблицею, то задача апроксимації полягає у визначенні достатньо простого виду функції (її аналітичного виразу), значення якої при
задана таблицею, то задача апроксимації полягає у визначенні достатньо простого виду функції (її аналітичного виразу), значення якої при 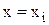 мало відрізнялись би від табличних даних. Якщо табличну залежність
мало відрізнялись би від табличних даних. Якщо табличну залежність 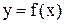 одержано в результаті експериментів, то задача апроксимації цієї залежності називається інакше підбором емпіричної функції. Геометрично задача апроксимації полягає в проведенні графіка функції f(x) якомога ближче до системи точок
одержано в результаті експериментів, то задача апроксимації цієї залежності називається інакше підбором емпіричної функції. Геометрично задача апроксимації полягає в проведенні графіка функції f(x) якомога ближче до системи точок 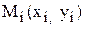 (на відміну від інтерполяції тут не ставиться умова повного збігання значень
(на відміну від інтерполяції тут не ставиться умова повного збігання значень 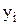 і
і 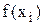 ).
).
Побудова емпіричної функції складається з двох етапів:
– вибору загального виду цієї функції;
– визначення кращих її параметрів.
5.4.1 Вибір виду емпіричної функції для нелінійних залежностей
Якщо аналітичний вид функції не відомий з фізичних міркувань, то підбір її є довільним і часто базується на досвіді дослідника.
В тому випадку, коли дослідні дані табл. 5.1 містять велику експериментальну похибку або коли не стоїть задача досягнення високої точності, можна обмежитися найпростішим видом формули, яка вміщує тільки два параметри 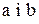 . В загальному випадку найбільш уживані поліноми виду (5.1) – (5.3).
. В загальному випадку найбільш уживані поліноми виду (5.1) – (5.3).
Нехай у є функцією однієї змінної х з двома параметрами а і b. За набір найпростіших функцій, з котрих будемо обирати емпіричну залежність, розглянемо
1) лінійну 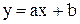 ;
;
2) показникову 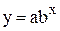 ;
;
3) дрібно-раціональну 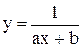 ;
;
4) логарифмічну 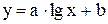 ;
;
5) степеневу 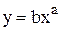 ( вона визначає параболічну залежність, якщо a > 0, і гіперболічну, якщо a < 0; якщо a = 0, то залежність вироджується в лінійну);
( вона визначає параболічну залежність, якщо a > 0, і гіперболічну, якщо a < 0; якщо a = 0, то залежність вироджується в лінійну);
6) гіперболічну 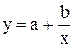 ;
;
7) дрібно-раціональну виду 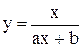 .
.
Для найкращого вибору виду аналітичної залежності 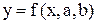 виконаємо наступні проміжні дії:
виконаємо наступні проміжні дії:
– табл. 5.1 зображаємо у вигляді графіка  ;
;
– на заданому відрізку зміни х 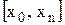 обираємо дві точки, які достатньо надійні і, за можливістю, далеко розташовані одна від другої, наприклад, крайні точки з координатами
обираємо дві точки, які достатньо надійні і, за можливістю, далеко розташовані одна від другої, наприклад, крайні точки з координатами 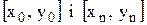 ;
;
– обчислюємо середні арифметичні 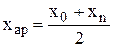 ,
, 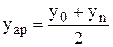 ;
;
середні геометричні 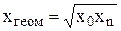 ,
, 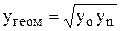 ;
;
середні гармонічні 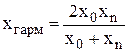 ,
, 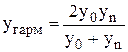 ;
;
– за обчисленими значеннями х знаходимо по графіку 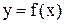 значення
значення 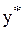
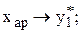
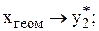
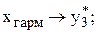
– порівнюємо знайдені з графіку значення 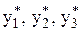 з обчисленими значеннями
з обчисленими значеннями 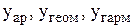 і оцінюємо наступні похибки результату порівняння:
і оцінюємо наступні похибки результату порівняння:
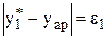 ,
, 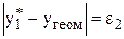 ,
, 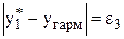 ,
,
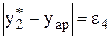 ,
, 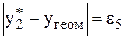 ,
, 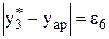 ,
, 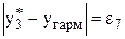 ;
;
– знаходимо з цих похибок мінімальну
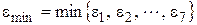
і робимо висновок про вид емпіричної функції у відповідності з табл. 5.4.
Таблиця 5.4 – Залежність виду функції 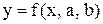 від
від 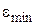
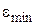
| 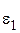
| 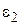
| 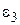
| 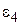
| 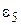
| 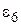
| 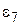
|
Вид
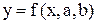
| 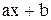
| 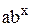
| 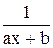
| 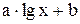
| 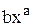
| 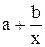
| 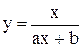
|

Перевірка відповідності виду емпіричної функції залежності, що задана таблицею 5.1, здійснюється за допомогою так званого методу вирівнювання,який полягає в наступному: припускають, що між х і у існує залежність означеного виду, знаходять деякі величини 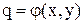 і
і 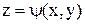 , які при зробленому припущенні зв‘язані лінійною залежністю (тобто перетворюють систему координат х0у, в якій залежність
, які при зробленому припущенні зв‘язані лінійною залежністю (тобто перетворюють систему координат х0у, в якій залежність 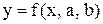 нелінійна, в систему координат
нелінійна, в систему координат 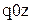 ,в якій ця залежність стає лінійною). Наприклад, якщо
,в якій ця залежність стає лінійною). Наприклад, якщо 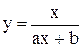 , то приймають
, то приймають 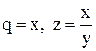 або
або 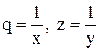 , обчислюють для заданих значень х і у (табл. 5.1) відповідні значення q i z, і зображують одержану залежність z(q) графічно. Якщо точки залежності z(q) лежать приблизно на прямій лінії, то робиться висновок, що вид емпіричної функції обрано вірно.
, обчислюють для заданих значень х і у (табл. 5.1) відповідні значення q i z, і зображують одержану залежність z(q) графічно. Якщо точки залежності z(q) лежать приблизно на прямій лінії, то робиться висновок, що вид емпіричної функції обрано вірно.
Для наведених вище нелінійних залежностей можна одержати лінійні залежності, якщо прийняти відповідні зв‘язки між змінними в координатах q0z і x0y (табл. 5.5).
Таблиця 5.5 – Зведення нелінійних залежностей до лінійних
| Нелінійна залежність | Лінійна залежність | Зв‘язок між змінними в координатах q0z і x0y |
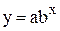
| 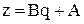
| 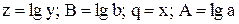
|
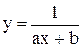
| 
| 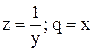
|
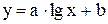
| 
| 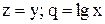
|
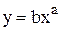
| 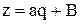
| 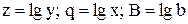
|
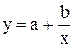
| 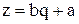
| 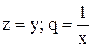
|
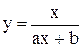
| 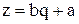
| 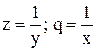
|
5.4.2 Уточнення коефіцієнтів емпіричної функції
Коефіцієнти а, в для емпіричних формул виду 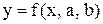 можна уточнити декількома методами. Нижче наведено один з них, який називають методом обраних точок.
можна уточнити декількома методами. Нижче наведено один з них, який називають методом обраних точок.
На кривій 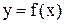 (або на прямій
(або на прямій  в методі вирівнювання) обирають дві довільні точки
в методі вирівнювання) обирають дві довільні точки 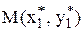 і
і 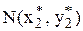 , складають систему рівнянь
, складають систему рівнянь
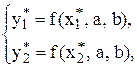
розв‘язують її відносно а, в і підставляють останні в функцію 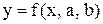 . Одержаний аналітичний вираз і являє собою розв‘язок задачі апроксимації функції, що задана таблицею.
. Одержаний аналітичний вираз і являє собою розв‘язок задачі апроксимації функції, що задана таблицею.
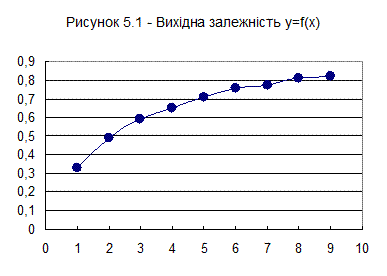
Приклад 5.1. Дані експерименту приведені в таблиці. Необхідно скласти емпіричну формулу.
Таблиця 5.6 – Експериментальні дані
| x | |||||||||
| y | 0,33 | 0,49 | 0,59 | 0,65 | 0,71 | 0,755 | 0,77 | 0,81 | 0,82 |
Будуємо графік (див. рис. 5.1).
Розраховуємо наступні параметри:
- середньоарифметичні значення
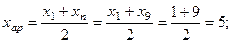
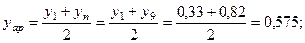
- середньогеометричні значення
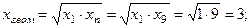
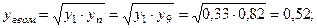
- середньогармонічні значення
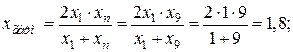
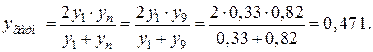
За графіком знаходимо значення у*:
хар = 5 →  ; хгеом = 3 →
; хгеом = 3 → 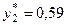 ; хгарм = 1,8 →
; хгарм = 1,8 → 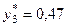 .
.
Розраховуємо похибки:
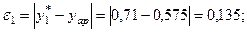
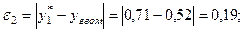
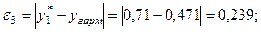
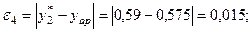
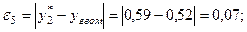
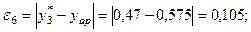
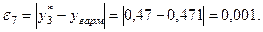
Найменше значення похибки 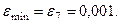 Згідно даних табл. 5.4 приймаємо вид емпіричної формули
Згідно даних табл. 5.4 приймаємо вид емпіричної формули 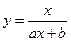 .
.
Для перевірки результату розглянемо нову лінійну функцію 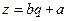 (див. табл. 5.5). Згідно табл.. 5.5 введемо нові змінні:
(див. табл. 5.5). Згідно табл.. 5.5 введемо нові змінні: 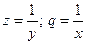 . Розрахуємо величини нових змінних. Вони приведені в табл. 5.7.
. Розрахуємо величини нових змінних. Вони приведені в табл. 5.7.
Таблиця 5.7 – Величини нових змінних
| x | |||||||||
| q = 1/х | 0,5 | 0,333 | 0,25 | 0,2 | 0,166 | 0,143 | 0,125 | 0,111 | |
| y | 0,33 | 0,49 | 0,59 | 0,65 | 0,71 | 0,755 | 0,77 | 0,81 | 0,82 |
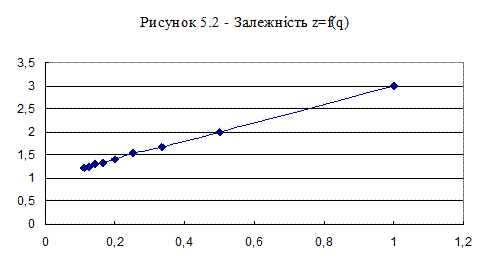
| z = 1/y | 1,66 | 1,54 | 1,41 | 1,32 | 1,3 | 1,24 | 1,22 |
Будуємо залежність z = f(q) (див. рис. 5.2). Точки графіка практично лежать на прямій. Тому вид функції обраний вірно.
Знайдемо коефіцієнти а і b функції 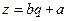 за методом обраних точок.
за методом обраних точок.
Обираємо першу і останню точку з табл. 5.7 з координатами z1 = 3, q1 = 1 i z9 = 1,22, q9 = 0,111. Складаємо систему рівнянь:
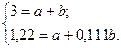
Розраховуємо коефіцієнти а і b: b = 2, а = 1. Таким чином емпірична формула має вигляд 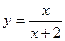 .
.
5.4.3 Апроксимація алгебричним поліномом
За вид емпіричної функції приймають поліном виду (5.1), тобто
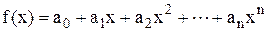 ,
,
де n ≤ m (число на одиницю менше кількості точок в табл. 5.1).
Для визначення коефіцієнтів полінома ( 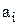 ) застосовують метод найменших квадратів. Для цього виконують наступне:
) застосовують метод найменших квадратів. Для цього виконують наступне:
– складають суму квадратів відхилень функції від табличних даних
 ;
;
– дорівнюють нулю частинні похідні функції S за незалежними змінними 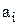

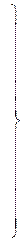
– «збирають» коефіцієнти при невідомих і одержують систему лінійних рівнянь, яку в компактному виді можна записати так:
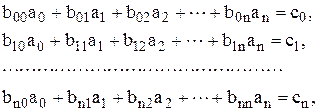
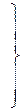 (5.15)
(5.15)
де 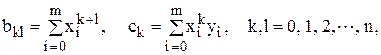 (5.16)
(5.16)
– розв‘язують систему (5.15) відносно  .
.
Наприклад, треба підібрати емпіричну формулу для функції, що задана табл. 5.6.
Таблиця 5.6 – Функція у(х)
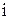
| 0 | 1 | 2 | 3 | 4 |
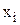
| 0,75 | 1,50 | 2,25 | 3,0 | 3,75 |
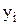
| 2,50 | 1,20 | 1,12 | 2,25 | 4,28 |
Приймемо за вид емпіричної формули алгебричний поліном. Щоб визначитися з порядком поліному, побудуємо графік за даними табл. 5.6 (рис. 5.1).
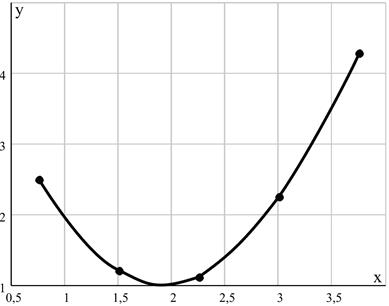
Рисунок 5.1 – Графік функції у(х)
З графіка видно, що функція має вид параболи, і тому її можна записати у вигляді 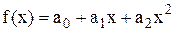 , тобто прийняти
, тобто прийняти 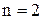 , що менше
, що менше 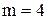 (див. найбільше значення і в табл.5.6).
(див. найбільше значення і в табл.5.6).
Далі розраховуємо коефіцієнти перед невідомими(аі) і вільні члени системи рівнянь (5.15) за виразами (5.16):
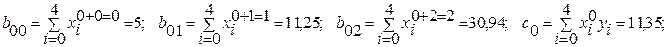
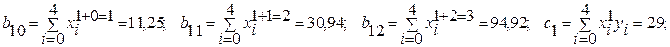
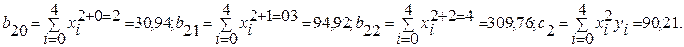
Таким чином система рівнянь в даному прикладі має вигляд
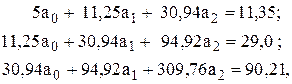
а її розв‘язок такий: 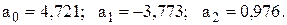
Отже, в результаті апроксимації функції у(х), що задана табл.5.6, одержано аналітичний вираз у вигляді поліному другого ступеня, а саме
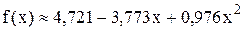 .
.
Оцінимо абсолютну 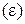 і відносну (
і відносну ( 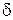 ) похибки апроксимації для точок завдання функції (табл. 5.7).
) похибки апроксимації для точок завдання функції (табл. 5.7).
Таблиця 5.7 – Оцінка похибок апроксимації
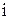
| 0 | 1 | 2 | 3 | 4 |
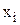
| 0,75 | 1,50 | 2,25 | 3,0 | 3,75 |
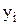
| 2,50 | 1,20 | 1,12 | 2,25 | 4,28 |
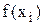
| 2,440 | 1,257 | 1,173 | 2,186 | 4,297 |
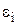
| -0,060 | 0,057 | 0,053 | -0,064 | 0,017 |
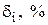
| 2,390 | 4,792 | 4,710 | 2,844 | 0,403 |
Дата добавления: 2016-02-02; просмотров: 2466;
