Формулювання задачі наближення функцій
Важним і цікавим є питання переходу від табличного способу завдання функції до аналітичного. Це дозволить уникнути вказаних вище недоліків табличного способу завдання функції.
Можна сформулювати таку задачу: нехай за допомогою таблиці (табл. 5.1) задано функцію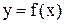 
. Знайти по можливості простий аналітичний вираз цієї функції.
Таблиця 5.1 – Функція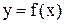
| x |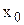 
| 
| 
| … | 
|
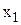
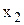
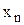
| y | 
| 
| 
| … | 
|
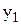
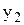
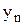
Спочатку задаються видом функції. Для цієї мети практично важливим є використання поліномів:
– алгебричного
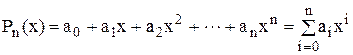; (5.1)
– тригонометричного
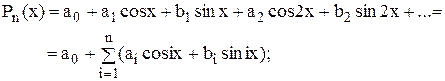(5.2)
– експоненціального
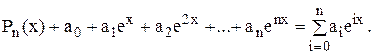(5.3)
Після того, як вид функції задано, стає задача визначення невідомих коефіцієнтів аі (bi) так, щоб досягти найменшого відхилення поліному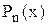 
від заданої функції у(х). Що стосується терміну «найменше відхилення», то може бути два випадки.
В першому ставиться задача точного відтворення всіх значень функції, що задані в табл. 5.1. Така задача називається інтерполяцією функції.
В другому випадку, коли табличні дані одержані, наприклад, в експерименті і містять експериментальні похибки, коефіцієнти полінома 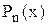знаходять так, щоб вказані в табл. 5.1 значення функції описувались наближено (нема сенсу повторювати помилки, які були допущені в експерименті). Така задача називається апроксимацією функції.
Дата добавления: 2016-02-02; просмотров: 573;