Лекция 7. РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Вводные замечания
Инженеру-исследователю в своей деятельности постоянно приходится сталкиваться с дифференциальными уравнениями, так как большая часть законов физики при их математическом моделировании сводится к дифференциальным уравнениям. В связи с этим решение дифуравнений является одной из важнейших математических задач.
Дифференциальным уравнением называется уравнение, в котором искомой является функция, а уравнение задает связь между значениями независимых переменных, искомой функцией и ее производными.
В зависимости от числа независимых переменных ДУ делятся на две различные группы: обыкновенные ДУ, содержащие одну независимую переменную, и уравнения в частных производных, содержащие несколько независимых переменных.
Рассмотрим обыкновенные ДУ.
Общий вид ОДУ
F (x, y, y’, …, y(n)) = 0, (7.1)
где x – независимая переменная;
y – функция;
y’,…, y(n) – производные;
n – наивысший порядок производной, порядок ДУ.
В ряде случаев из общей записи ДУ (7.1) удается выразить старшую производную в явном виде, например,
y” = f (x, y, y’ ).
Такая форма записи называется уравнением, разрешенным относительно старшей производной.
Решением ДУ (7.1) называется всякая функция y = φ(x), которая после ее подстановки в уравнение превращает его в тождество.
Дифференциальное уравнение, как правило, имеет бесконечное множество решений, зависящее от некоторого количества (определяемого порядком ДУ) произвольных постоянных С1, С2, …, Сn.
Общее решение ОДУ (7.1) имеет вид
у = φ(x, С1, С2, …, Сn ).
Частное решение ОДУ получается из общего, если произвольным постоянным придать определенные значения, например, для уравнения первого порядка:
- общее решение у = φ(x, С);
- частное решение, если С = С0 (определенное значение) у = φ(x, С0).
Исследователя обычно интересует частное решение. Чтобы его получить, необходимо учитывать не только особенности изменения явления, описываемого ДУ (7.1), но и дополнительные условия, которые характеризуют это явление. Количество дополнительных условий должно быть равно количеству произвольных постоянных, то есть порядку n.
Дифференциальное уравнение вместе с дополнительными условиями называется задачей. Если х является временем (что характерно для эволюционных или динамических процессов), то необходимо учесть состояние в начальный момент времени х0, а если х – координата, которая может изменяться от а до b (например, прогиб балки под действием постоянной силы), то необходимо учесть состояние системы (балки) на ее границах – в точках а и b.
Таким образом, возможно существование двух типов дополнительных условий и соответственно двух типов задач:
1. Начальные условия (всего n условий) у(х0)= у0, 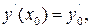 …,
…, 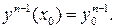 Задача решения ОДУ (7.1) с начальными условиями, заданными в одной точке, называется задачей Коши.
Задача решения ОДУ (7.1) с начальными условиями, заданными в одной точке, называется задачей Коши.
2. Граничные (краевые) условия (всего n условий) у(а)= уа, 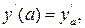 …, у(b)= уb,
…, у(b)= уb,  …. Задача решения ОДУ (7.1) с граничными условиями называется краевой или двухточечной задачей.
…. Задача решения ОДУ (7.1) с граничными условиями называется краевой или двухточечной задачей.
7.2 Как решать ДУ
Целью решения ДУ является получение функции у = φ(x). Эта функция может быть задана графическим, аналитическим и табличным способом. Поэтому методы решения ДУ (7.1) делятся на графические, аналитические и численные.
Графические методы используются при качественном исследовании ДУ и состоят в построении интегральной кривой.
Аналитические методы дают решение уравнения в виде формулы и делятся на точные и приближенные.
Точные методы рассматриваются в вузовском курсе. Они дают точные решения, но могут быть использованы для узкого класса задач.
Приближенные аналитические методы дают функцию, являющуюся аппроксимацией точного решения. Для получения такой функции либо заменяют исходное ДУ близким к нему, но допускающим аналитическое решение, либо задаются видом решения.
Основной проблемой, возникающей при этом является проблема точности. Выход состоит в использовании идеи о разбиении области изменения независимой переменной х на малые отрезки и решении ДУ на каждом отрезке.
Этот подход иллюстрируем следующим рисунком.
1 – точное решение уравнения; 2 – аппроксимация решения линейной функцией для всей области; 3 – аппроксимация решения при разбиении области изменения х[a, b] на мелкие отрезки.
Видно, что замена линейной функции 2 кусочно-линейной функцией 3 значительно повышает точность решения.
Дальнейшее развитие рассматриваемой идеи привело к появлению численных методов решения ДУ, результатом которых является таблица значений функции в определенных точках (узлах).
7.3 Одношаговые методы решения задачи Коши
Задачу Коши можно сформулировать для ДУ первого порядка следующим образом.
Пусть дано ДУ y’ = f (x, y) c начальным условием y(x0) = y0. Требуется найти функцию y = f (x), удовлетворяющую как указанному уравнению, так и начальному условию.
Обычно численное решение этой задачи получают, вычисляя сначала значение производной в точке х0, а затем задавая малое приращение х и переходя к новой точке x1 = x0 + h. Положение новой точки определяется по наклону кривой, вычисленному с помощью ДУ.
Таким образом, график численного решения представляет собой последовательности коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y = f (x).
Сам численный метод определяет порядок действия при переходе от данной точки кривой к следующей.
В одношаговых методах для нахождения следующей точки на кривой y= f (x) требуется информация лишь об одном предыдущем шаге. К одношаговым относятся метод Эйлера и методы Рунге-Кутта.
7.3.1 Метод Эйлера (схема ломаных)
Является сравнительно грубым и применяется в основном для ориентировочных расчетов. Основан на разложении функции у в ряд Тейлора в окрестности точки х0:
y (x0 + h) = y(x0) + h y’(x0) + 1/2 h2 y”(x0) + …
Если шаг интегрирования h мал, то члены ряда, содержащие h во второй и более высоких степенях, малы. Поэтому ими можно пренебречь. Тогда
y (x0 + h) = y(x0) + h y’(x0).
Значение y’(x0) находим из ДУ, подставив в него начальное условие.
Этот процесс можно продолжить, используя следующее соотношение
yi +1 = yi + h f (xi, yi), i = 0, 1, …, n – 1.
Графически метод представляется следующим образом
 Погрешность этого метода пропорциональна шагу h.
Погрешность этого метода пропорциональна шагу h.
Большая погрешность – главный недостаток этого метода. Точность метода Эйлера можно повысить, улучшив аппроксимацию производной. Это можно сделать, используя среднее значение производной в начале и конце интервала.
Пример 7.1.
Решить ДУ 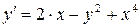 на интервале [0, 1] с шагом h = 0,25 методом Эйлера. Начальные условия: y(x0) = у0 = 0.
на интервале [0, 1] с шагом h = 0,25 методом Эйлера. Начальные условия: y(x0) = у0 = 0.
Решение выполняется по формуле yi +1 = yi + h f (xi, yi).
Первый шаг: i = 0, x0 = 0, y0 = 0
у0 +1=1 = y0 + h (2x0 – y20 + х40) = 0 + 0,25·(2∙0 – 02 + 04) = 0.
Второй шаг: i = 1, x1 = x0 + h = 0 + 0,25 = 0,25, y1 = 0
у1 +1=2 = y1 + h (2x1 – y21 + х41) = 0 + 0,25·(2∙0,25 – 02 + 0,254) = 0,126.
Третий шаг: i = 2, x2 = x1 + h = 0,25 + 0,25 = 0,5, y2 = 0,126
у2 +1=3 = y2 + h (2x2 – y22 + х42) = 0,126 + 0,25·(2∙0,5 – 0,1262 + 0,54) = 0,3877.
Четвертый шаг: i = 3, x3 = x2 + h = 0,5 + 0,25 = 0,75, y3 = 0,3877
у3 +1=4 = y3 + h (2x3 – y23 + х43) = 0,3877 + 0,25·(2∙0,75 – 0,38772 + 0,754) = 0,8042.
Метод Эйлера может быть применен к решению систем дифференциальных уравнений и ДУ высших порядков. Однако в последнем случае ДУ должны быть приведены к системе ДУ первого порядка.
Пусть задана система двух уравнений первого порядка
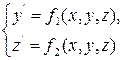
с начальными условиями у(х0) = у0, z(х0) = z0.
Приближенные значения у(хi) ≈ уi и z(хi) ≈ zi находятся по формулам
yi+1 = yi + Δ yi, zi+1 = zi + Δ zi,
где
Δ yi = hf1(xi, yi, zi), Δ zi = hf2(xi, yi, zi) i = 0, 1, 2, …
Пример 7.2.
Применяя метод Эйлера, решить систему ДУ 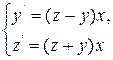 при начальных условиях у(0) = 1,0000 z(0) = 1,0000 на отрезке [0, 0,6] с шагом h = 0,1. Вычисления вести с одним запасным знаком.
при начальных условиях у(0) = 1,0000 z(0) = 1,0000 на отрезке [0, 0,6] с шагом h = 0,1. Вычисления вести с одним запасным знаком.
Покажем часть вычислений:
- первый шаг: i = 0, х0 = 0, y0 = 1,0000, z0 = 1,0000,
y0’= (z0 – y0)·x0 = (1 – 1)·0 = 0; Δ y0 = h y0’ = 0,1·0 = 0;
z0’= (z0 + y0)·x0 = (1 + 1)·0 = 0; Δ z0 = h z0’ = 0,1·0 = 0;
- второй шаг: i = 1, х1 = х0 + h = 0 + 0,1 = 0,1;
y1 = y0 + Δ y0∙ = 1,0000 + ·0 = 1,0000;
z1 = z0 + Δ z0∙ = 1,0000 + 0 = 1,0000;
y1’= (z1 – y1)·x1 = (1 – 1)·0,1 = 0; Δ y1 = h y1’ = 0,1·0 = 0;
z1’= (z1 + y1)·x1 = (1 + 1)·0,1 = 0,2; Δ z1 = h z1’ = 0,1·0,2 = 0,02;
- третий шаг: i = 2, х2 = х1 + h = 0,1 + 0,1 = 0,2;
y2 = y1 + Δ y1∙ = 1,0000 + 0 = 1,0000;
z2 = z1 + Δ z1∙ = 1,0000 + 0,02 = 1,02;
y2’= (z2 – y2)·x2 = (1,02 – 1)·0,2 = 0,004; Δ y2 = h y2’ = 0,1·0,004 = 0,0004;
z2’= (z2 + y2)·x2 = (1,02 + 1)·0,2 = 0,404; Δ z2 = h z2’ = 0,1·0,404 = 0,0404.
Решение на остальных шагах приведено в табл.7.1
Таблица 7.1 – Решение системы ДУ
| i | xi | yi+1 = yi-1+Δ yi-1 | yi’= (zi – yi)·xi | Δ yi = yi’·h | zi+1 = zi-1+Δ zi-1 | zi’= (zi + yi)·xi | Δ zi = zi’·h |
| 0,1 | 1,0000 | 1,0000 | |||||
| 0,2 | 1,0000 | 1,0000 | 0,2000 | 0,0200 | |||
| 0,3 | 1,0000 | 0,004 | 0,0004 | 1,0200 | 0,4040 | 0,0404 | |
| 0,4 | 1,0004 | 0,018 | 0,0018 | 1,0604 | 0,6182 | 0,0618 | |
| 0,5 | 1,0022 | 0,048 | 0,0048 | 1,1222 | 0,8498 | 0,0850 | |
| 0,6 | 1,0070 | 0,1001 | 0,0100 | 1,2072 | 1,01071 | 0,1107 | |
| 0,7 | 1,0170 | 1,3179 |
Пример 7.3.
Применяя метод Эйлера, составить на отрезке [1; 1,5] таблицу значений ДУ 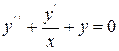 при начальных условиях у(1) = 0,77, у’(1) = - 0,44 с шагом h = 0,1.
при начальных условиях у(1) = 0,77, у’(1) = - 0,44 с шагом h = 0,1.
С помощью подстановки у’ = z, у’’ = z’ заменим данное уравнение системой уравнений
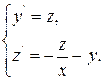
при начальных условиях у(1) = 0,77, z(1) = - 0,44
Результаты расчета приведены в табл. 7.2
Таблица 7.1 – Решение системы ДУ
| i | xi | yi | yi’= z | Δ yi = yi’·h | zi | zi’= - zi / xi - yi | Δ zi = zi’·h |
| 1,0 | 0,77 | -0,44 | -0,044 | -0,44 | -0,33 | -0,033 | |
| 1,1 | 0,726 | -0,473 | -0,0473 | -0,473 | -0,296 | -0,03 | |
| 1,2 | 0,679 | -0,503 | -0,0503 | -0,503 | -0,26 | -0,026 | |
| 1,3 | 0,629 | -0,529 | -0,0529 | -0,529 | -0,222 | -0,022 | |
| 1,4 | 0,576 | -0,551 | -0,0551 | -0,551 | -0,183 | -0,018 | |
| 1,5 | 0,521 |
7.3.2 Метод Эйлера Коши
Сначала вычисляется значение функции в следующей точке по методу Эйлера
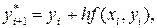
которое затем используется для вычисления приближенного значения производной в конце интервала 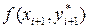 .
.
Вычислив среднее арифметическое между значениями производной (наклонами ломаных) в начале и конце интервала, найдем более точное значение уi+1 (формула Эйлера-Коши):
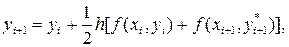
где хi+1 = хi + h.
Принцип, на котором основано улучшение метода Эйлера, можно пояснить и иначе – на основе использования разложения функции в ряд Тейлора. Точность повышается за счет того, что сохраняются в разложении члены, содержащие производные более высоких порядков, чем первый. Для улучшения метода Эйлера надо знать вторую производную. Ее можно аппроксимировать конечной разностью
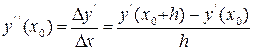
Если ее подставить в ряд Тейлора, то результатом будет формула Эйлера-Коши.
Пример 7.4.
Решить ДУ 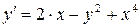 на интервале [0, 1] с шагом h = 0,25 методом Эйлера - Коши. Начальные условия: y(x0) = у0 = 0.
на интервале [0, 1] с шагом h = 0,25 методом Эйлера - Коши. Начальные условия: y(x0) = у0 = 0.
Решение выполняется по формулам:
у*i +1 = yi + h f (xi, yi), 
Первый шаг: i = 0, x0 = 0, y0 = 0
у*1 = y0 + h (2x0 – y20 + х40) = 0 + 0,25·(2∙0 – 02 + 04) = 0;
x1 = x0 + h = 0 + 0,25 = 0,25
у1 = у0 + 0,5h [(2x0 – y20 + х40) + (2x1 – ( y1*)2 + х41)] =
= 0 + 0,5·0,25·[(2∙0 – 02 + 04) + (2∙0,25 – 02 + 0,254) = 0,063;
Второй шаг: i = 1, x1 = 0,25, y1 = 0,063
y*2 = y1 + h (2x1 – y21 + х41) = 0,063 + 0,25·(2∙0,25 – 0,0632 + 0,254) = 0,188;
x2 = x1 + h = 0,25 + 0,25 = 0,5
у2 = у1 + 0,5h [(2x1 – y21 + х41) + (2x2 – ( y2*)2 + х42)] =
= 0,063 + 0,5·0,25·[(2∙0,25 – 0,0632 + 0,254) + (2∙0,5 – 0,1882 + 0,54)] = 0,254;
Третий шаг: i = 2, x2 = 0,5, y2 = 0,254
y*3 = y2 + h (2x2 – y22 + х42) = 0,254 + 0,25·(2∙0,5 – 0,2542 + 0,54) = 0,5035:
x3 = x2 + h = 0,5 + 0,25 = 0,75
у3 = у2 + 0,5h f [(2x2 – y22 + х42) + (2x3 – ( y3*)2 + х43)] =
= 0,254 + 0,5·0,25·[(2∙0,5 – 0,2542 + 0,54) + (2∙0,75 – 0,50352 + 0,754)] = 0,574.
7.3.3 Усовершенствованный метод Эйлера
Сущность усовершенствованного метода Эйлера состоит в следующем: сначала вычисляются вспомогательные значения искомой функции yi+1/2 в точках xi+1/2 = xi + h/2 помощью формулы
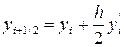 ,
,
затем находят значение f (x,y) в средней точке  и определяют
и определяют
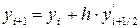 .
.
Оценка погрешности в точке хi может быть получена с помощью «двойного просчета»: расчет повторяют с шагом h/2 и погрешность более точного 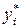 ( при шаге h/2) оценивают приближенно по формуле
( при шаге h/2) оценивают приближенно по формуле
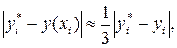
где у(х) – точное решение ДУ.
Пример 7.5.
Проинтегрировать усовершенствованным методом Эйлера ДУ y’ = y – x при начальных условиях х0 = 0, у0 = 1,5 на отрезке [0, 1], приняв h = 0,25.
Первый шаг: i = 0, x0 = 0, y0 = 1,5.
y’0+1 = y0 - x0 = 1,5 – 0 = 1,5; 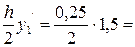 0,1875;
0,1875;
x0+1/2 = x0 + 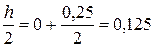 ; y0+1/2 = y0 +
; y0+1/2 = y0 + 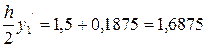 ;
;
y’0+1/2 = y0+1/2 – x0+1/2 = 1,6875 – 0,125 = 1,5625;  0,3906;
0,3906;
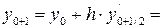 1,5 + 0,3906 = 1,8906;
1,5 + 0,3906 = 1,8906;
Второй шаг: i = 1, x1 = x0 + h = 0 + 0,25 = 0,25; y1 = 1,8906.
y’2 = y1 – x1 = 1,8906 – 0,25 = 1,6406; 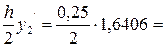 0,2051;
0,2051;
x1+1/2 = x1 + 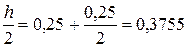 ;
;
y1+1/2 = y1 +  ;
;
y’1+1/2 = y1+1/2 – x1+1/2 = 2,0957 – 0,375 = 1,7207; 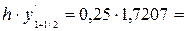 0,4302;
0,4302;
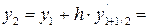 1,8906 + 0,4302 = 2,3208.
1,8906 + 0,4302 = 2,3208.
За повышение точности приходится расплачиваться дополнительными затратами времени на вычисление функции 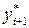 .
.
Более высокая точность может быть получена, если улучшить аппроксимацию производной, сохраняя большее число членов ряда Тейлора.
7.3.4 Методы Рунге-Кутта
Метод Рунге-Кутта является одним из методов повышенной точности. Он имеет много общего с методом Эйлера. Метод Эйлера можно считать методом Рунге-Кутта первого порядка ( в разложении в ряд Тейлора остается только первая производная).
Пусть требуется найти численное решение уравнения y’ = f (x, y) на отрезке [a, b] с начальными условиями у(х0) = у0.
Разобьем отрезок [a, b] на n равных частей с точками xi = x0 + i·h (i = 0, 1,…, n), где h = (b - a)/n – шаг интегрирования. В методе Рунге-Кутта, так же как и в методе Эйлера, последовательные значения yi искомой функции у определяются по формуле
yi +1 = yi + Δ yi.
Если разложить функцию у в ряд Тейлора и ограничиться членами до h4 включительно, то приращение функции Δ y можно представить в виде
 , (7.2)
, (7.2)
где производные 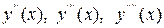 находят последовательным дифференцированием из уравнения y’ = f (x, y).
находят последовательным дифференцированием из уравнения y’ = f (x, y).
Вместо непосредственных вычислений по формуле (7.2) в методе Рунге-Кутта определяют четыре числа:
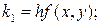
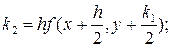
(7.3)

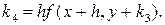
Можно доказать, что если числам k1, k2, k3, k4 придать соответственно вес 1/6; 1/3; 1/3; 1/6, то средневзвешенное этих чисел, т.е.

с точностью до четвертых степеней равно значению Δу, вычисленному по формуле (7.2)
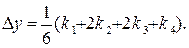 (7.4)
(7.4)
Таким образом, для каждой пары текущих значений xi и yi по формулам (7.3) определяют значения
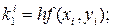
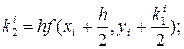
(7.5)
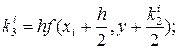
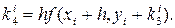
по формуле (7.4) находят

Метод Рунге-Кутта имеет порядок точности h4 на всем отрезке [a, b]. Оценка точности этого метода затруднительна. Грубую оценку погрешности можно получить с помощью «двойного просчета» по формуле
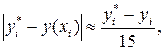
где у(хi) – значение точного решения ДУ в точке хi, а 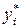 и уi – приближенные значения, полученные с шагом h/2 и h.
и уi – приближенные значения, полученные с шагом h/2 и h.
Если ε – заданная точность решения, то число n (число делений) для определения шага интегрирования h = (b - a)/n выбирается таким образом, чтобы
h4 < ε.
Однако шаг расчета можно менять при переходе от одной точки к другой. Для оценки правильности выбора шага h используется равенство
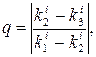
где q должно быть равно нескольким сотым, в противном случае шаг h уменьшают.
Пример 7.6.
Дано ДУ у’ = у – х, удовлетворяющее начальному условию у(0) = 1,5. Вычислить с точностью до 0,01 решение этого уравнения на интервале [0, 1,5]. Вычисление выполнить методом Рунге-Кутта с двумя запасными знаками.
Выбираем начальный шаг из условия h4 < ε = 0,01:
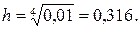
Для удобства вычислений примем h = 0,25.
Первый шаг: i = 0, x0 = 0, y0 = 1,5.
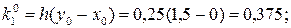
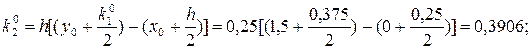


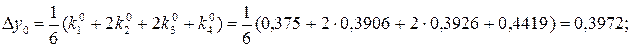
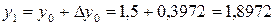 .
.
Второй шаг: i = 1, x1 = x0 + h = 0 + 0,25 = 0,25, y1 = 1,8972.

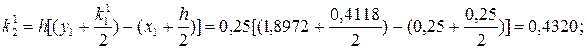

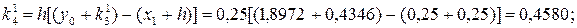
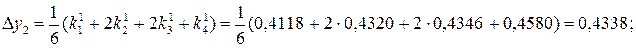
 .
.
Метод Рунге-Кутта может быть применен к решению систем ДУ.
Пусть дана система ДУ первого порядка:
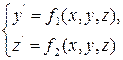
с начальными условиями х = х0, у(х0) = у0, z(х0) = z0.
В этом случае параллельно определяются числа Δуi, Δzi:
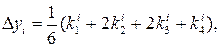
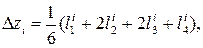
где

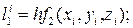
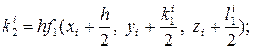
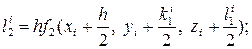
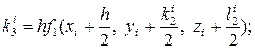

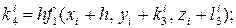
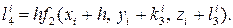
Тогда получим решение системы
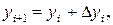
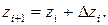
Пример 7.7.
Задана система ДУ

при начальных условиях х0 = 0,5; у0 = 1,0; z0 = 1,0. Найти решение системы при х = 0,6. Вычисления вести с пятью знаками после запятой.
Выбираем шаг h = 0,1 и определим коэффициенты:
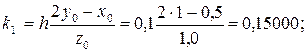
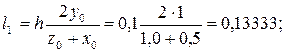
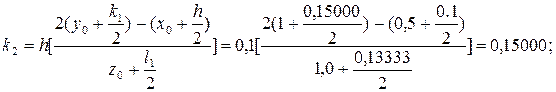


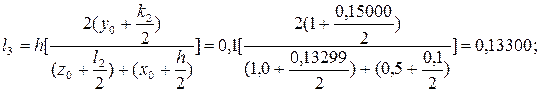
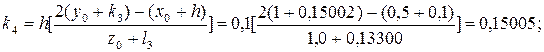
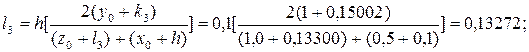
Вычисляем приращение искомых функций
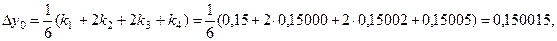

Значение искомых функций в точке х = 0,6
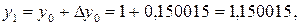

7.3.5 Общая характеристика одношаговых методов
Одношаговым методам присущи следующие общие черты:
1. Чтобы получить информацию в новой точке надо иметь данные лишь в одной предыдущей точке. Это свойство называется «самостартованием» - «self-starting behavior».
2. В основе всех одношаговых методов лежит разложение функции в ряд Тейлора, в котором сохраняются члены, содержащие шаг h в степени до m включительно. Целое число m называется порядком метода.
3. Все одношаговые методы не требуют действительного вычисления производных – вычисляется лишь сама функция, однако могут потребоваться значения в нескольких промежуточных точках.
4. Свойство называется «самостартования» позволяет легко менять величину шага.
Дата добавления: 2016-02-02; просмотров: 1229;
