Чисельне інтегрування
6.1.1 Вступні зауваження
Нехай на відрізку 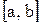 задана функція
задана функція 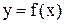 (рис.6.1). Розіб‘ємо відрізок
(рис.6.1). Розіб‘ємо відрізок 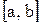 на
на 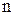 елементарних відрізків
елементарних відрізків 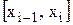 , причому
, причому  ,
, 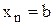 . На кожному
. На кожному
Рисунок 6.1 – До поняття визначеного інтеграла
відрізку оберемо довільну точку 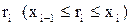 і знайдемо добуток
і знайдемо добуток 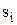 значення функції в цій точці
значення функції в цій точці 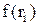 на довжину елементарного відрізка
на довжину елементарного відрізка 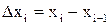 :
:

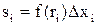 .
.
Складемо суму всіх таких добутків – інтегральну суму
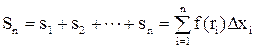 . (6.1)
. (6.1)
Визначеним інтегралом від функції 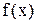 на відрізку
на відрізку 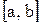 називають межу інтегральної суми при необмеженому збільшенні кількості точок розбиття; при цьому довжина найбільшого з елементарних відрізків наближається до нуля:
називають межу інтегральної суми при необмеженому збільшенні кількості точок розбиття; при цьому довжина найбільшого з елементарних відрізків наближається до нуля:
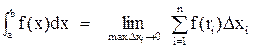 . (6.2)
. (6.2)
Якщо функція 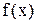 неперервна на
неперервна на 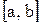 , то межа інтегральної суми існує і не залежить ні від способу розбиття відрізка
, то межа інтегральної суми існує і не залежить ні від способу розбиття відрізка 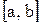 на елементарні відрізки, ні від вибору точок
на елементарні відрізки, ні від вибору точок 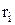 .
.
Якщо підінтегральна функція задана в аналітичному виді, визначений інтеграл можна обчислити з допомогою невизначеного інтеграла (вірніше першообразної). Визначений інтеграл дорівнює прирощенню першообразної F(x) на відрізку інтегрування і обчислюється за формулою Ньютона-Лейбниця
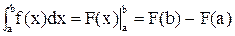 . (6.3)
. (6.3)
На практиці формулою (6.3) часто не можна скористуватися з двох причин:
– вид f(x) не допускає безпосереднього інтегрування, тобто першообразну не можна виразити в елементарних функціях;
– функція f(x) задана у вигляді таблиці.
В цих випадках застосовуються методи чисельного інтегрування. Вони засновані на апроксимації підінтегральної функції деякими більш простими виразами, наприклад, інтерполяційними многочленами, що дозволяє наближено замінити визначений інтеграл інтегральною сумою. В залежності від способу її обчислення одержують різні формули чисельного інтегрування, так звані квадратурні формули (формули прямокутників, трапецій, парабол і інші).
6.2 Метод прямокутників і трапецій
Метод прямокутників (найпростіший) безпосередньо використовує заміну визначеного інтеграла інтегральною сумою. За точки ri можуть бути обрані ліві (ri = xi-1) або праві(ri = xi) границі елементарних відрізків. При позначенні
f(xi) = yi, Δxi = hi
одержимо наступні формули метода прямокутників відповідно до указаних випадків (ліві, праві):
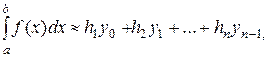 (6.4)
(6.4)
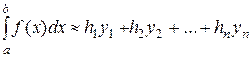 (6.5)
(6.5)
Широко поширеним і більш точним є вид формули прямокутників, що використовує значення функції в середніх точках елементарних відрізків (в півцілих вузлах)
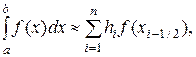 (6.6)
(6.6)
де xi-1/2 = (xi-1+xi)/2 = xi-1+hi/2, i = 1,2,…,n.
Найчастіше під методом прямокутників розуміють алгоритм (6.6). Його ще називають методом середніх.
Метод трапеційвикористовує лінійну інтерполяцію, тобто графік y = f(x) зображується у вигляді ламаної, що з‘єднує точки (xi, yi). В цьому випадку площа всієї фігури складається з площ елементарних прямолінійних трапецій (див. рис.6.2).
Рисунок 6.2 – До методу трапецій
Площа кожної такої трапеції дорівнює
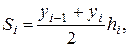 і = 1,2, ..., n.
і = 1,2, ..., n.
Формула трапецій для чисельного інтегрування має вигляд
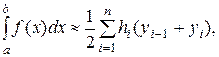 (6.7)
(6.7)
Частным случаем рассмотренных формул является их применение при численном интегрировании с постоянным шагом hi = h = const. Формулы (6.6) и (6.7) принимают вид:
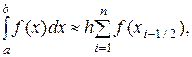 (6.8)
(6.8)
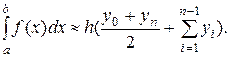 (6.9)
(6.9)
На основании формул прямоугольников и трапеций можно получить уточненные значения интегралов, если учесть характер погрешностей этих формул.
Погрешности:
- для метода средних прямоугольников
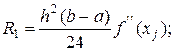
- для метода левых и правых прямоугольников
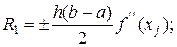
- для формулы трапеций
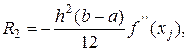
где 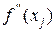 - максимальное значение второй производной на интервале [a, b] (a≤ xj ≤ b).
- максимальное значение второй производной на интервале [a, b] (a≤ xj ≤ b).
Уточненные значения интегралов получаются, если к выражениям (6.8) и (6.9) добавить соответствующие погрешности R1 и R2. Величины R1 и R2 в выражениях для вычисления интеграла называют остаточными членами.
Погрешность численного интегрирования зависит от шага (h) разбиения, и, следовательно, уменьшая его можно добиться большей точности. Однако, если функция задана в виде таблицы, то приходится ограничиваться данным множеством точек.
Повышение точности интегрирования может быть достигнуто за счет повышения степени используемых интерполяционных многочленов. Например, использование квадратичной интерполяции.
6.3 Метод Симпсона (парабол)
Разобьем отрезок интегрирования [a, b] на четное число n равных частей с шагом h. На каждом отрезке [х0, х2], [х2, х4],…, [хi-1, х i+1], [хn-2, х n] подинтегральную функцию f(x) заменим интерполяционным многочленом второй степени:
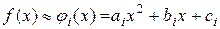
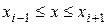 .
.
Рисунок 6.3 – К методу парабол
Коэффициенты этих квадратных трехчленов (  ) могут быть найдены из условия равенства многочлена в точках хi, соответствующим табличным данным yi.
) могут быть найдены из условия равенства многочлена в точках хi, соответствующим табличным данным yi.
В качестве функции φi(x) можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через точки с координатами (хi-1, у i-1), (хi, уi ) и (хi+1, у i+1)
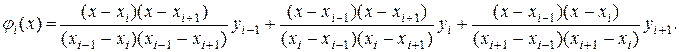
Элементарная площадь Si вычисляется с помощью определенного интеграла. Учитывая, что  , получим:
, получим:
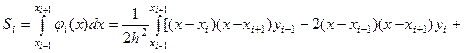
+  .
.
Проведя такие вычисления для каждого элементарного отрезка [хi-1, хi+1], просуммируем полученные выражения. Результат суммирования записывается следующим образом:
 .
.
Выражения для S принимается в качестве значения определенного интеграла (формула Симпсона):
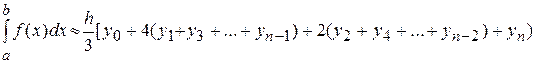 (6.10)
(6.10)
Погрешность метода Симпсона определяется по формуле
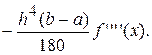
6.4 Обобщенная формула численного интегрирования Ньютона Котеса
Формула Симпсона является частным случаем обобщенной формулы численного интегрирования Ньютона-Котеса, которая имеет вид:
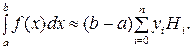 (6.11)
(6.11)
При различных n получают различные квадратурные формулы Ньютона – Котеса. Коэффициенты Hi, называемые коэффициентами Котеса, определяются из соотношения:
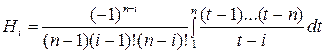 , n > 1, i = 1, 2,…, n; 0! = 1. (6.12)
, n > 1, i = 1, 2,…, n; 0! = 1. (6.12)
Эти коэффициенты обладают следующими полезными при вычислении свойствами:
1. Симметричные коэффициенты (первый и n-ый, второй и (n – 1)-й и т.д.) равны между собой:
Hi = Hn+1-i.
2. Сумма всех коэффициентов равна единице
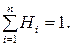
Получим коэффициенты квадратурной формулы при n = 3. Применяя формулу (6.12), получим:
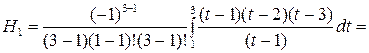
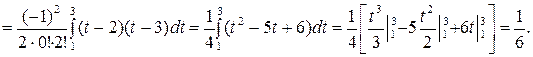
Далее, используя свойства коэффициентов Котеса, найдем
H3 = H1 = 1/6, H2 = 1 – (H1 + H3) = 1 – (1/6+1/6) = 2/3.
В табл. 6.1 приведены значения коэффициентов Котеса для n = 2, 3, 4, 5, 6.
Таблица 6.1 - Коэффициенты Котеса
| n i | ||||||
| 1/2 | 1/2 | |||||
| 1/6 | 4/6 | 1/6 | ||||
| 1/8 | 3/8 | 3/8 | 1/8 | |||
| 7/90 | 32/90 | 12/90 | 32/90 | 7/90 | ||
| 19/288 | 75/288 | 50/288 | 50/288 | 75/288 | 19/288 |
6.5 Практические способы оценки погрешности интегрирования
Погрешность интегрирования можно оценить:
- по остаточному члену;
- по правилу Рунге.
6.5.1 По остаточному члену
Если при вычислении остаточного члена возникают трудности с нахождением максимума производной (подинтегральная функция сложна или задана таблично), то возможно применение приближенных формул, выраженных через конечные разности:
- для левых и правых прямоугольников
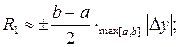
- для формулы трапеций

- для формулы Симпсона
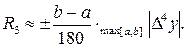
Для определения максимальных по модулю конечных разностей составляется (по табличной функции) таблица конечных разностей нужного порядка.
6.5.2 По правилу Рунге
Обозначим через Ih и Ih/2 приближенные значения интеграла, определенные с шагом h и h/2. Тогда абсолютная погрешность интегрирования приближенно оценивается по формуле (правило Рунге):
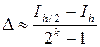 ,
,
где k – порядок остаточного члена, используемой формулы. Например, для формулы трапеций k = 2, для формулы Симпсона k = 4. То есть k – это порядок производной.
6.6 Выбор шага интегрирования
Задача заключается в выборе шага h, который обеспечивает заданную точность ε вычисления интеграла по выбранной формуле.
6.6.1 Выбор шага по остаточному члену
Используя формулу соответствующего остаточного члена R, выбирают такой шаг, чтобы обеспечивалось неравенство:

Затем с полученным шагом вычисляют интеграл по квадратурной формуле. Вычисления следует производить с таким числом цифр, чтобы погрешность округления не превышала ε.
6.6.2 Метод последовательного удвоения числа шагов
Вычисляют интеграл по выбранной формуле дважды: сначала с шагом h (Ih), затем с шагом h/2 ( Ih/2), то есть удваивают число вычислений n. Если
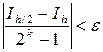 ,
,
0то полагают J ≈ Jh/2. Если условие не выполняется, то расчет повторяют с шагом h/4. В качестве начального шага иногда можно рекомендовать число, близкое к 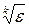 .
.
Пример
Рассчитать методом Симпсона определенный интеграл от функции f (x) = (x +1)·sin (x) на интервале [1,6; 2,4]. Принять ε = 0,001.
Выбираем начальный шаг с учетом требований о четности числа точек разбиения. Для формулы Симпсона k = 4, поэтому 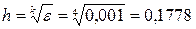 .
.
Вычисляем количество шагов
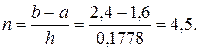
Округляем n в большую сторону до четного значения: n = 6.
Составим таблицу значений подинтегральной функции yi = f (xi) с шагом

Таблица 6.2 – Значения функции f (x) = (x +1)·sin (x) при n = 6.
| i | |||||||
| xi | 1,6 | 1,73 | 1,87 | 1,99 | 2,13 | 2,27 | 2,4 |
| yi | 2,5989 | 2,6973 | 2,7421 | 2,7279 | 2,6506 | 2,5074 | 2,2966 |
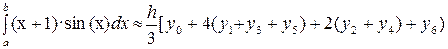 ;
;
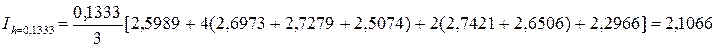
Удвоим число точек: n = 12 и шаг 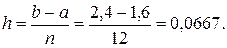 Новые значения функции приведены в табл. 6.3.
Новые значения функции приведены в табл. 6.3.
Таблица 6.3 – Значения функции f (x) = (x +1)·sin (x) при n = 12.
| i | |||||||
| xi | 1,6 | 1,67 | 1,73 | 1,8 | 1,87 | 1,93 | 2,0 |
| yi | 2,5989 | 2,6544 | 2,6973 | 2,7268 | 2,7421 | 2,7427 | 2,7279 |
Продолжение табл. 6.3
| i | ||||||
| xi | 2,07 | 2,13 | 2,2 | 2,27 | 2,33 | 2,4 |
| yi | 2,6973 | 2,6506 | 2,5873 | 2,5074 | 2,4105 | 2,2966 |
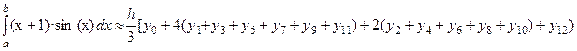
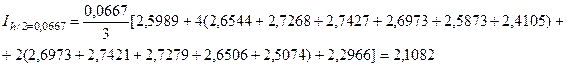
Оценим погрешность по правилу Рунге
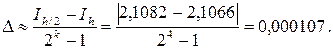
Пример
Рассчитать методом Ньютона-Котеса определенный интеграл 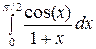 , выбрав n = 4.
, выбрав n = 4.
Для n = 4 формула Ньютона-Котеса имеет вид
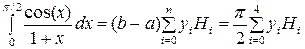 .
.
Согласно табл. 6.1 коэффициенты Котеса равны: H0 = 7/90; H1 = 32/90 = 16/45; H2 = 12/90 = 2/15; H3 = H1 = 16/45; H4 = H0 = 7/90.
Определяем шаг интегрирования: 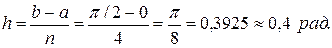
Вычисляем значения функции (см. табл. 6.4).
Таблица 6.4 – Значения функции
| i | |||||
| xi | 0,4 | 0,8 | 1,2 | 1,6 | |
| yi | 1,0 | 0,659 | 0,393 | 0,174 | |
| Коэф. | 7/90 | 16/45 | 2/15 | 16/45 | 7/90 |
Подставив коэффициенты в формулу для вычисления интеграла, получим:
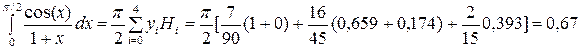 .
.
Дата добавления: 2016-02-02; просмотров: 819;
