Відокремлення коренів
Найбільш поширеними методами відокремлення коренів є аналітичний і графічний.
Аналітичний метод передбачає розрахунок значень функції (і її знаків) в ряді точок. Для знаходження відрізків ізоляції коренів рівняння (2.1) в межах зони існування коренів [RН, RВ] достатньо визначити точки 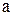 і
і 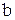 , для яких f(a)·f(b) < 0, тобто f(a) і f(b) мають протилежні знаки. Для того, щоб гарантувати, що на відрізку [a, b] є тільки один корінь, необхідно розраховувати значення функції у великій кількості точок, що буває недоцільно.
, для яких f(a)·f(b) < 0, тобто f(a) і f(b) мають протилежні знаки. Для того, щоб гарантувати, що на відрізку [a, b] є тільки один корінь, необхідно розраховувати значення функції у великій кількості точок, що буває недоцільно.
Графічний метод відокремлення коренів існує в двох різновидах:
1) будують графік функції 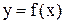 , знаходять точки перетину графіка з віссю абсцис і визначають навколо цих точок відрізки [a, b];
, знаходять точки перетину графіка з віссю абсцис і визначають навколо цих точок відрізки [a, b];
2) всі члени рівняння (2.1) поділяють на дві групи, одну з яких записують в лівій, а другу – в правій частині рівняння, тобто зображують його у вигляді
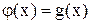
і будують графіки функцій 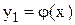 і
і 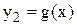 ; далі знаходять межі (відрізки [a, b]), в яких містяться абсциси точок перетину графіків функцій y1 і y2.
; далі знаходять межі (відрізки [a, b]), в яких містяться абсциси точок перетину графіків функцій y1 і y2.
2.3 До запитання про розв‘язання алгебричних рівнянь
2.3.1 Визначення кількості дійсних коренів
Наближено визначити кількість дійсних додатних коренів алгебричного рівняння
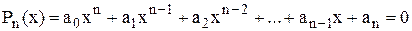 (2.2)
(2.2)
можна за допомогою правила Декарта: кількість дійсних додатних коренів алгебричного рівняння 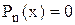 із дійсними коефіцієнтами дорівнює числу змін знаку в послідовності коефіцієнтів рівняння, або на парне число менше (коефіцієнти, що дорівнюють нулю не враховуються).
із дійсними коефіцієнтами дорівнює числу змін знаку в послідовності коефіцієнтів рівняння, або на парне число менше (коефіцієнти, що дорівнюють нулю не враховуються).
Кількість від‘ємних коренів алгебричного рівняння дорівнює числу змін знаку в послідовності коефіцієнтів рівняння 
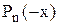 або на парне число менше.
або на парне число менше.
2.3.2 Визначення області існування коренів
Розглянемо два з декількох методів визначення верхньої межі додатних коренів рівняння 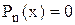 .
.
Метод Лагранжа. Якщо коефіцієнти многочлена 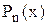 відповідають умовам a0 > 0, a1, a2, …,am-1 ≥ 0, am < 0, то верхня межа додатних коренів рівняння (2.2) визначається за формулою
відповідають умовам a0 > 0, a1, a2, …,am-1 ≥ 0, am < 0, то верхня межа додатних коренів рівняння (2.2) визначається за формулою
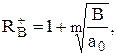 (2.3)
(2.3)
де В – найбільша із абсолютних величин від‘ємних коефіцієнтів;
m – ступінь х при першому від’ємному коефіцієнті а.
Метод Ньютона. Якщо при х = С многочлен 
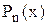 і його похідні
і його похідні 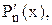
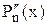 , … приймають додатні значення, то С є верхньою межею додатних коренів рівняння
, … приймають додатні значення, то С є верхньою межею додатних коренів рівняння 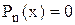 .
.
Існує засіб визначення інших меж дійсних коренів з використанням методів визначення верхньої межі додатних коренів 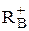 .
.
Якщо
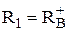 рівняння
рівняння 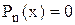 ,
,
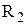 —″— —″—
—″— —″— 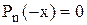 ,
,
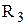 —″— —″—
—″— —″— 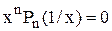 ,
,
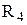 —″— —″—
—″— —″— 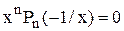 ,
,
то всі відмінні від нуля дійсні корені рівняння 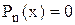 (якщо вони існують) лежать у середині інтервалів
(якщо вони існують) лежать у середині інтервалів
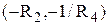 і
і 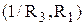 .
.
Визначимо, наприклад, межі додатних і від‘ємних коренів рівняння
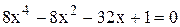 .
.
Знайдемо за методом Лагранжа R1, R2, R3, R4. У многочлені 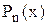 a0 = 8
a0 = 8
> 0; а1 = 0; а2 = -8 < 0; a3 = -32; a4 = 1, m = 2. Отже, 
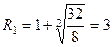
 .
.
Для многочлена
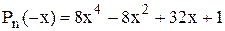
Аналогічно знаходимо 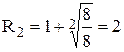 .
.
Далі, для многочлена
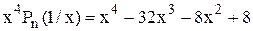
a0 = 1 > 0; a1 = -32 < 0, тобто m = 1, B = 32 i R3 = 1 + 32 = 33.
Зрештою, для многочлена
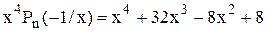
Маємо a0 = 1 > 0; a1 = 32; a2 = -8; a3 = 0; a4 = 8, тобто m = 2; B = 8. Тому 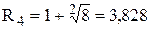 .
.
Отже, якщо задане рівняння має дійсні корені, вони обов‘язково лежать у межах (-2; -1 / 3,828) і (1 / 33; 3).
2.3.3 Обчислення значень многочлена. Схема Горнера
Розв‘язування алгебричних рівнянь як на етапі відокремлення коренів, так і при їх уточненні потребує багаторазових обчислень значень 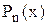 . Тому важливе значення має побудова найбільш економічних (з точки зору кількості операцій) алгоритмів.
. Тому важливе значення має побудова найбільш економічних (з точки зору кількості операцій) алгоритмів.
 Припустимо, що треба розрахувати значення многочлена
Припустимо, що треба розрахувати значення многочлена 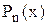 (див. (2.2)) при
(див. (2.2)) при 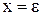 . Обчислення
. Обчислення 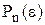 вигідно проводити для перетвореного запису (2.2) до наступного вигляду
вигідно проводити для перетвореного запису (2.2) до наступного вигляду
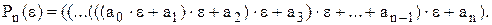 (2.4)
(2.4)
Послідовне обчислення чисел (n множень і n додавань)
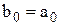
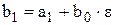
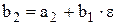
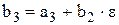
· · · · · · ·
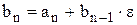
дає значення 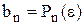 .
.
 Алгоритм розрахунку
Алгоритм розрахунку 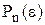 , який складено на основі виразу (2.4) називають схемою Горнера. Саме у вигляді схеми розрахунки розташовують так:
, який складено на основі виразу (2.4) називають схемою Горнера. Саме у вигляді схеми розрахунки розташовують так:
|
|
|
|
|





 a0 a1 a2 a3 … an-1 an
a0 a1 a2 a3 … an-1 an



 ε b0·ε b1·ε b2·ε … bn-2·ε bn-1·ε
ε b0·ε b1·ε b2·ε … bn-2·ε bn-1·ε
b0 b1 b2 b3 … bn-1 bn.
В першому рядку записані коефіцієнти многочлена 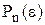 . В третій рядок переносять a0 = b0 і далі суму добутку кожного коефіцієнта bi на ε із аі+1.
. В третій рядок переносять a0 = b0 і далі суму добутку кожного коефіцієнта bi на ε із аі+1.
Уточнення коренів
До найбільш поширених методів уточнення коренів алгебричних і трансцендентних рівнянь відносять методи:
– половинного ділення (інші назви: бісекції, дихотомії);
– хорд (помилкового положення);
– дотичних (Ньютона);
2.4.1 Метод половинного ділення
Суть методу, в тому, що відрізок ізоляції кореня [а, b] ділять навпіл точкою х1 = 0,5(а+b) і обчислюють f(x1). Якщо f(x1) = 0, то х1 є точне значення кореня. Якщо f(x1) ¹ 0, але (b-a) £ 2ε (ε – задана точність визначення кореня) , то х1 – є наближене значення кореня що знайдено із заданою точністю. Якщо f(x1) ¹ 0 і
 (b-a) > 2ε, тоді розглядають той з двох відрізків [a, x1] і [x1, b], на кінцях якого функція f(x1) набуває значень протилежних знаків (рис. 2.1). Цей відрізок знов ділять навпіл точкою х2 (друге наближення кореня) і так само визначають, чи не перевищує абсолютна похибка наближення кореня х2 величини ε. Очевидно, що знаходження чергового наближення кореня після n ітерацій здійснюється за виразом
(b-a) > 2ε, тоді розглядають той з двох відрізків [a, x1] і [x1, b], на кінцях якого функція f(x1) набуває значень протилежних знаків (рис. 2.1). Цей відрізок знов ділять навпіл точкою х2 (друге наближення кореня) і так само визначають, чи не перевищує абсолютна похибка наближення кореня х2 величини ε. Очевидно, що знаходження чергового наближення кореня після n ітерацій здійснюється за виразом
xn+1 = 0,5(an + bn). (2.5)
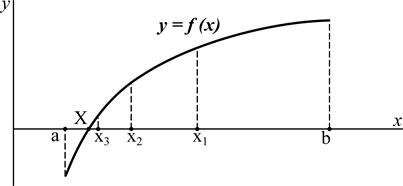
Рисунок 2.1 – Графічне зображення суті методу половинного ділення
Алгоритм методу половинного ділення можна зобразити таким чином:
Завдання a, b, ε;
R = f(a);
► x = 0,5(a + b);
f(x);
якщо 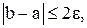 то х – корінь;
то х – корінь;
 да, то
да, то 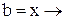 ►
► 
 інакше R·f(x) < 0 ?
інакше R·f(x) < 0 ?
ні, то 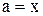 , R = f(x)
, R = f(x) 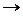 ►.
►.
2.4.2Метод хорд
В цьому методі відрізок С ділять не навпіл, а у відношенні f(a) / f(b). Суть методу полягає в тому, що за наближення до кореня приймаються значення x1, x2, x3, …, xn точок перетину хорди з віссю абсцис (рис. 2.2).
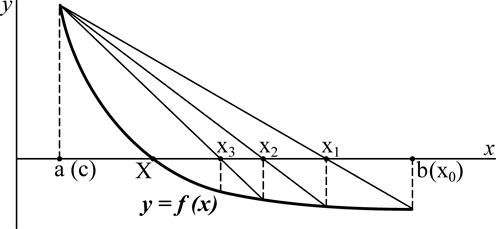
Рисунок 2.2 – Графічне зображення ідеї методу хорд
Наступне наближення кореня визначається за формулою

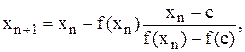 (2.6)
(2.6)
де с – так звана нерухома точка, за яку приймається той з кінців відрізка [а, b], для котрого знак функції збігається зі знаком другої похідної ( 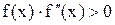 ). На рис. 2.2 с = а. Другий кінець відрізка [а, b] приймається за початкове наближення х0, що використовується формулою (2.6).
). На рис. 2.2 с = а. Другий кінець відрізка [а, b] приймається за початкове наближення х0, що використовується формулою (2.6).
Ітераційний процес закінчується при виконанні умови
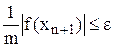 ,
,
де 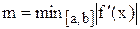 – найменше значення модуля першої похідної на відрізку [а, b].
– найменше значення модуля першої похідної на відрізку [а, b].
Для використання методу хорд необхідно для інтервалу [a, b] обчислити
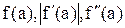 і
і 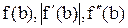 . За допомогою одержаних значень визначити величини m, c, x0 таким чином:
. За допомогою одержаних значень визначити величини m, c, x0 таким чином: 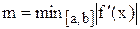 ; якщо f(a) і
; якщо f(a) і 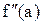 мають однаковий знак, то с = а і х0 = b (відповідно, якщо однаковий знак мають f(b) і
мають однаковий знак, то с = а і х0 = b (відповідно, якщо однаковий знак мають f(b) і 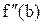 , то с = b і х0 = а).
, то с = b і х0 = а).
Далі алгоритм методу хорд виглядає так:
Завдання ε, m, c, x0;
f(c);
R = f(x0);
► x = 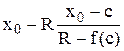 ;
;
f(x);
якщо 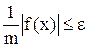 , то х – корінь;
, то х – корінь;
інакше: R = f(x), x0 = x 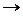 ►.
►.
2.4.3 Метод дотичних
Метод полягає в побудові ітераційної послідовності

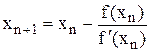 , (2.7)
, (2.7)
що збігається до кореня рівняння f(x) = 0.
Достатні умови збіжності метода: послідовність (2.7) збігається до дійсного значення кореня рівняння f(x) = 0, якщо початкове наближення кореня (х0) належить інтервалу [а, b], на котрому 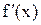 і
і 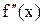 зберігають свій знак і задовольняється умова
зберігають свій знак і задовольняється умова 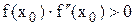 .
.
За х0 приймають той з кінців відрізка [а, b], для якого 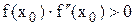 (в методі хорд це нерухома точка).Метод допускає просту геометричну інтерпретацію, а саме: якщо через точку з координатами
(в методі хорд це нерухома точка).Метод допускає просту геометричну інтерпретацію, а саме: якщо через точку з координатами 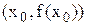 провести дотичну, то абсциса точки перетину цієї дотичної з віссю х і є чергове наближення кореня рівняння f(x) = 0 (рис. 2.3).
провести дотичну, то абсциса точки перетину цієї дотичної з віссю х і є чергове наближення кореня рівняння f(x) = 0 (рис. 2.3).
Ітерації продовжуються до виконання умови
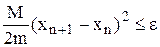 ,
,
Де М – найбільше значення модуля другої похідної на відрізку [а, b],
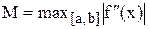 .
.
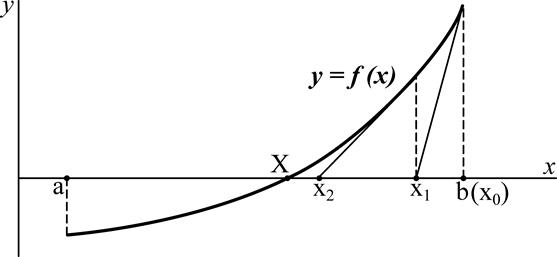
Рисунок 2.3 – Графічне подавання ідеї методу дотичних
Для використання методу дотичних необхідно для інтервалу [a, b] обчислити 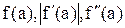 і
і 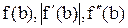 . За допомогою одержаних значень визначити величини m, М, x0 таким чином:
. За допомогою одержаних значень визначити величини m, М, x0 таким чином: 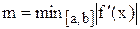 ;
; 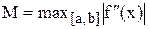 , якщо f(a) і
, якщо f(a) і 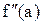 мають однаковий знак, то х0 = а.
мають однаковий знак, то х0 = а.
Далі алгоритм методу дотичних може виглядати так:
Завдання ε, m, М, x0;
► х = х0;
f(x);
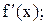
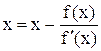 ;
;
якщо 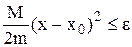 , то х – корінь;
, то х – корінь;
інакше: x0 = x 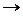 ►.
►.
Метод дотичних має високу швидкість збіжності, однак недоліком його є необхідність обчислення похідної 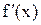 на кожній ітерації. Якщо
на кожній ітерації. Якщо 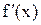 мало змінюється на відрізку [а, b], то можна значно зменшити обсяг обчислень, якщо скористуватися модифікованим методом Ньютона з використанням формули
мало змінюється на відрізку [а, b], то можна значно зменшити обсяг обчислень, якщо скористуватися модифікованим методом Ньютона з використанням формули

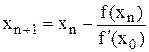 .
.
2.4.4 Комбінований метод хорд і дотичних
Методи хорд і дотичних дають наближення кореня з різних боків. Тому їх часто поєднують і уточнення кореня відбувається скоріше.
 На кожній ітерації використовується спочатку формула (2.7), потім – формула (2.6), в якій за с приймають значення x, що розраховано на даному кроці за формулою(2.7). Процес закінчується, коли
На кожній ітерації використовується спочатку формула (2.7), потім – формула (2.6), в якій за с приймають значення x, що розраховано на даному кроці за формулою(2.7). Процес закінчується, коли 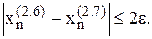 Остаточне значення кореня визначається формулою
Остаточне значення кореня визначається формулою
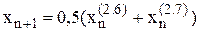 , (2.8)
, (2.8)
де 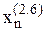 і
і 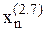 – наближення кореня, які розраховані відповідно за формулами (2.6) і (2.7).
– наближення кореня, які розраховані відповідно за формулами (2.6) і (2.7).
2.4.5 Метод ітерацій
Для знаходження кореня методом ітерацій (простих) рівняння f(x) = 0 приводять до вигляду 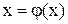 так, щоб виконувалось співвідношення
так, щоб виконувалось співвідношення 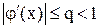 , яке є достатньою умовою збіжності ітераційного процесу.
, яке є достатньою умовою збіжності ітераційного процесу.
На інтервалі [а, b] обирають початкове наближення х0 (бажано в середині інтервалу, щоб похибка заокруглення не вивела за межі [а, b], де виконуються умови збіжності); наступні наближення визначаються за формулою

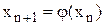 (2.9)
(2.9)
доти, поки не буде виконано умову
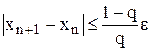 (2.10)
(2.10)
(можна прийняти 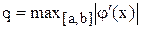 ).
).
З геометричної точки зору коренем рівняння 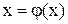 є абсциса точки перетину кривої
є абсциса точки перетину кривої 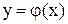 і прямої
і прямої 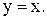
Характер зміни 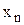 в процесі обчислень за формулою (2.9), а також вид умови закінчення ітерацій залежать від знака і абсолютної величини
в процесі обчислень за формулою (2.9), а також вид умови закінчення ітерацій залежать від знака і абсолютної величини 
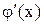 на інтервалі [а, b].
на інтервалі [а, b].
– Якщо 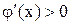 , то послідовні наближення сходяться до кореня монотонно. При цьому, якщо q £ 0,5 за умову закінчення ітерацій можна прийняти
, то послідовні наближення сходяться до кореня монотонно. При цьому, якщо q £ 0,5 за умову закінчення ітерацій можна прийняти
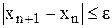 . (2.11)
. (2.11)
– Якщо 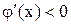 , то послідовні наближення коливаються навколо дійсного значення кореня і при цьому також можна користуватися умовою (2.11). Таким чином, умову (2.10) необхідно використовувати тільки в тих випадках, коли
, то послідовні наближення коливаються навколо дійсного значення кореня і при цьому також можна користуватися умовою (2.11). Таким чином, умову (2.10) необхідно використовувати тільки в тих випадках, коли 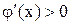 і
і 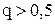 .
.
Не завжди легко обрати функцію 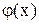 , що задовольняє умові збіжності.
, що задовольняє умові збіжності.
Розглянемо один з алгоритмів переходу від рівняння 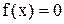 до рівняння
до рівняння 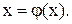 Помножимо ліву і праву частини рівняння
Помножимо ліву і праву частини рівняння 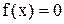 на довільну константу h і додамо до обох частин невідоме х
на довільну константу h і додамо до обох частин невідоме х
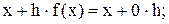
при цьому корені вихідного рівняння не зміняться.
Позначимо 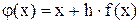 і одержимо
і одержимо 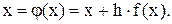
Очевидно, що при будь-яких 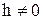 рівняння
рівняння 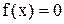 і
і 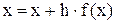 рівносильні. Константу
рівносильні. Константу 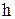 бажано обрати такою, щоб
бажано обрати такою, щоб 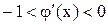 , тоді буде забезпечена збіжність ітераційного процесу.
, тоді буде забезпечена збіжність ітераційного процесу.
Похідна 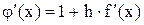 . Найбільша швидкість збіжності має місце при
. Найбільша швидкість збіжності має місце при 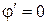 , тоді
, тоді 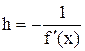 і ітераційна формула (2.9) переходить у формулу Ньютона (метода дотичних)
і ітераційна формула (2.9) переходить у формулу Ньютона (метода дотичних)
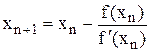 .
.
Дата добавления: 2016-02-02; просмотров: 3392;
