МЕТОДИ РОЗВ'ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ
Моделювання лінійних електричних кіл засновано на законах Кірхгофа (перший закон – слідство принципу безперервності електричного струму; другий – слідство закону збереження енергії) і Ома.
Метою розрахунку є визначення струмів у всіх гілках, напруг в вузлах, потужностей електроприймачів.
Математична модель електричного кола надається еквівалентною схемою що містить m гілок і n вузлів, а також ЕРС всіх джерел, внутрішніми і зовнішніми опорами.
Послідовність розрахунку лінійного електричного кола з використанням законів Кірхгофа наступна:
а) для кожної гілки вводять позначення протікаючого через неї струму і стрілками на схемі указують умовні позитивні напрями цих струмів;
б) для n-1 вузлів складають рівняння на підставі першого закону Кірхгофа; для одного з вузлів таке рівняння не складають, оскільки воно є слідством вже написаних рівнянь;
в) беруть взаємно незалежні контури кола (це означає, що в кожному новому контурі хоча б в одній з гілок струм не входить в попередньо розглянуті контури), в кожному з цих контурів вибирають умовний позитивний напрям обходу і позначають його на схемі;
г) для вибраних контурів складають рівняння по другому закону Кірхгофа з урахуванням напряму обходу; при правильному виборі контурів їх число повинно дорівнювати m - n + 1; при цьому загальна кількість рівнянь повинно складати m, тобто по числу невідомих величин;
д) вирішують отриману систему з m рівнянь одним з методів обчислювальної математики.
Якщо розраховане значення струму в даній гілці є позитивним, то це означає, що дійсний напрям струму співпадає з вибраним раніше і навпаки.
Складання системи лінійних рівнянь (СЛР) розглядається на прикладі схеми розгалуженого електричного кола постійного струму (рис.3.1). Параметри резисторів складають відповідно: 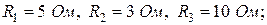 ЕРС джерел, що містяться у гілках схеми:
ЕРС джерел, що містяться у гілках схеми: 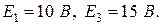
Згідно законів Кірхгофа, алгоритму розрахунку, схеми електричного кола і напрямку обходу контурів система лінійних алгебраїчних рівнянь (СЛАР) має вигляд (3.1), де невідомі - це струми в гілках, коефіцієнти при невідомих – параметри елементів, а вільні члени – ЕРС джерел:
 |
Рисунок 3.1
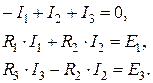 (3.1)
(3.1)
Надалі, СЛАР, що отримано, розв'язується різними методами.
3.1 Форми запису систем лінійних алгебричних рівнянь і способи розв'язання матричних рівнянь
В загальному вигляді система n лінійних алгебричних рівнянь з n невідомими записується так:

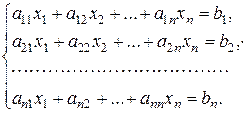 (3.2)
(3.2)
Коротко систему (3.2) можна записати в такому вигляді:
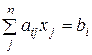 (і = 1, 2, …, n). (3.3)
(і = 1, 2, …, n). (3.3)
З використанням матричних позначень систему (3.2) можна записати в наступному виді:
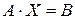 , (3.4)
, (3.4)
або в розгорнутому вигляді:
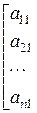
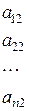


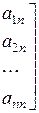 ·
· 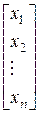 =
= 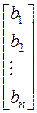 . (3.5)
. (3.5)
Взагалі, розглядаються три види матричних рівнянь і способи їх розв'язання.
Матричне рівняння виду 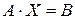 . Для розв'язання такого рівняння треба помножити зліва обидві його частини на обернену матрицю
. Для розв'язання такого рівняння треба помножити зліва обидві його частини на обернену матрицю 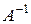 :
: 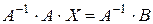 . При цьому добуток
. При цьому добуток 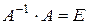 (одинична матриця), отже,
(одинична матриця), отже, 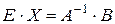 , звідки
, звідки
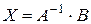 . (3.6)
. (3.6)
Матричне рівняння виду 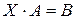 . Треба помножити справа обидві його частини на
. Треба помножити справа обидві його частини на 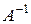 :
: 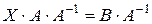 . Виходить:
. Виходить: 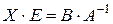 , звідки
, звідки
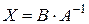 . (3.7)
. (3.7)
Матричне рівняння виду 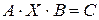 . При помноженні обох частин рівняння – зліва на
. При помноженні обох частин рівняння – зліва на 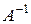 , а справа на
, а справа на 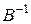 виходить
виходить 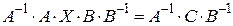 , або
, або 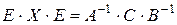 , звідки
, звідки
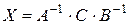 . (3.8)
. (3.8)
3.2 Методи розв'язування СЛАР
Методи поділяють на прямі, які використовують для обчислення невідомих кінцеві співвідношення (формули) і чисельні, які, в загальному випадку, поділяються на ітераційні методи і методи мінімізації.
Прямі методи дають розв'язок після виконання заздалегідь відомої кількості операцій. Ці методи прості і універсальні. Разом з тим їм властиві такі недоліки:
– вони потребують зберігання в оперативній пам'яті відразу всієї матриці;
– не враховують структуру матриці – нульові елементи також зберігаються в пам‘яті і над ними проводяться арифметичні дії;
– відбувається накопичення похибок в процесі розв'язування (хоч прямі методи і називають точними), тому що обчислення на будь-якому етапі використовують результати попередніх операцій.
У зв‘язку з цим прямі методи використовують для порівняно невеликих (n < 200) систем із щільно заповненою матрицею і не близьким до нуля визначником.
Чисельніметоди, якітераційні,так імінімізації – це методи послідовних наближень. Вони потребують деякого наближеного розв'язку – початкового наближення. Далі за визначеним алгоритмом виконується ряд ітерацій до одержання результату з необхідною точністю. Методи мають перевагу перед прямими в наступному:
– потребують зберігання не всієї матриці системи, а лише декількох векторів з n компонент; іноді елементи матриці можна зовсім не зберігати, а обчислювати їх при необхідності;
– похибки кінцевих результатів не накопичуються, тому що в кожній ітерації використовується результат тільки попередньої і не використовуються раніше виконані обчислення.
Але при цих перевагах збіжність ітераційних методів може бути дуже повільною.
3.2.1 Прямі методи розв'язування СЛАР
Прямі методи розглядаються у вузівському курсі «Вища математика» і в даному курсі про них тільки згадується.
Отже, перший з прямих методів – це метод, що використовує формули Крамера, де невідомі визначаються як відношення визначників.
Найбільш поширеним прямим методом розв‘язання СЛАР на ЕОМ є метод послідовного виключення невідомих (метод Гаусса) і його модифікації.
Один з різновидів методу Гаусса (компактна схема Гаусса) – метод LU–перетворення.
Компактні схеми Гауса використовуються для СЛАР із розрідженими матрицями довільної структури. В цих схемах застосовується тріангуляція матриць (трикутна декомпозиція) – суть якої полягає в перетворенні матрично-векторного рівняння (1.5) в рівняння з трикутними матрицями (методику перетворення квадратної матриці на добуток двох трикутних наведено нижче).
Порядок дій в методі LU–перетворення наступний:
а) виконується заміна матриці А на добуток двох трикутних матриць L і U; (в матриці U діагональні елементи дорівнюють одиницям);
б) розв'язується відносно Y рівняння 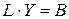 ;
;
в) розв'язується відносно X рівняння 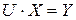 .
.
Дата добавления: 2016-02-02; просмотров: 1637;
