Синус, косинус, тангенс, котангенс числа.
- Поскольку для радианной меры угла характерно нахождение величины угла через длину дуги, то можно графически изобразить связь радианной меры и градусной. Для этого изобразим окружность радиуса 1 на координатной плоскости таким образом, чтобы ее центр находился в начале координат. Положительные углы будем откладывать против часовой стрелки, а отрицательные - по часовой.
- Градусную меру угла обозначим как обычно, а радианную – при помощи дуг, лежащих на окружности. P0 – начало отсчета угла. Остальные – точки 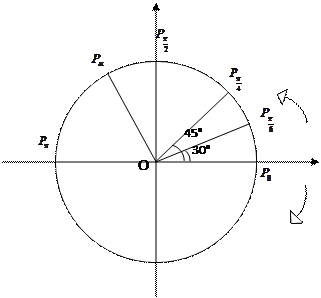
 пересечения сторон угла с окружностью.
пересечения сторон угла с окружностью.
Определение: Окружность радиуса 1 с центром в начале координат называется единичной окружностью.
- Кроме обозначения углов у данной окружности есть еще одна особенность: на ней можно изобразить единственной точкой данной окружности любое действительное число. Это можно сделать точно также, как на числовой прямой. Мы как будто сгибаем числовую прямую таким образом, чтобы она лежала на окружности.
P0 – начало отсчета, точка числа 0. Положительные числа отмечают в положительном направлении (против часовой стрелки), а отрицательные – в отрицательном (по часовой стрелке). Отрезок равный α есть дуга P0Pα.
- Любое число можно изобразить точкой Pα на окружности, причем эта точка для каждого числа единственна, но можно заметить, что множеству чисел α+2πn, где n-целое число, соответствует одна и та же точка Pα.
- Каждая точка имеет свои координаты, которые имеют специальные названия.
Определение: Косинусом числа α называется абсцисса точки, соответствующей числу α на единичной окружности.
Определение: Синусом числа α называется ордината точки, соответствующая числу α на единичной окружности.
Pα (cosα, sinα).
- Из геометрии:
Косинус угла в прямоугольном треугольнике – отношение противолежащего угла к гипотенузе. В данном случае гипотенуза равна 1, то есть косинус угла измеряется длиной отрезка ОА.
Синус угла в прямоугольном треугольнике – отношение прилежащего катета к гипотенузе. То есть синус измеряется длиной отрезка ОВ.
- Запишем определения тангенса и котангенса числа.
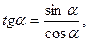 где cos α≠0
где cos α≠0
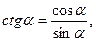 где sin α≠0
где sin α≠0
- Задача нахождения значений синуса, косинуса, тангенса и котангенса произвольного числа путем применения некоторых формул сводится к нахождению значений sinα, cosα, tgα и ctgα, где 0≤α≤π/2.
Таблица основных значений тригонометрических функций
| α | π/6 | π/4 | π/3 | π/2 | π | 2 π | |
| 0° | 30° | 45° | 60° | 90° | 180° | 360° | |
| sin α | 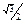
| 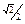
| 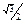
| ||||
| cos α | 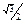
| 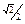
| ½ | -1 | |||
| tg α | 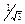
| 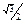
| - | ||||
| ctg α | - | 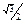
| 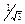
| - | - |
Найти значение выражений:
а) 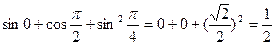
б) 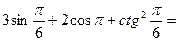
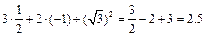
Дата добавления: 2016-01-30; просмотров: 7623;
