Уравнение поверхности и линии в пространстве
Поверхность в пространстве 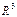 можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О есть геометрическое место всех точек пространства, находящихся от точки О на расстоянии R.
можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О есть геометрическое место всех точек пространства, находящихся от точки О на расстоянии R.
Прямоугольная система координат Оxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел x, y и z – их координатами: абсциссой, ординатой и аппликатой. Координатами точки 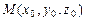 в пространстве (рис. V.3) являются числа, соответствующие точкам пересечения координатных плоскостей Oxy, Oxz, Oyz с координатными осями Ox, Oy, Oz.
в пространстве (рис. V.3) являются числа, соответствующие точкам пересечения координатных плоскостей Oxy, Oxz, Oyz с координатными осями Ox, Oy, Oz.
Свойство, общее для всех точек поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности [4].
Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение 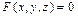 с тремя переменными, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные x, y и z в уравнении поверхности называются текущими координатами точек поверхности. Линию в пространстве можно рассматривать как линию пересечения двух поверхностей или как геометрическое место точек, принадлежащее обеим поверхностям.
с тремя переменными, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные x, y и z в уравнении поверхности называются текущими координатами точек поверхности. Линию в пространстве можно рассматривать как линию пересечения двух поверхностей или как геометрическое место точек, принадлежащее обеим поверхностям.
Если 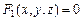 и
и 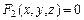 – уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:
– уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными: 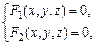 – уравнение линии в пространстве.
– уравнение линии в пространстве.
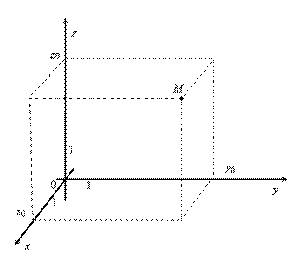
Рис. V.3
Например, 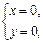 есть уравнение оси Оz.
есть уравнение оси Оz.
Линию в пространстве можно задать как траекторию движения некоторой точки. В этом случае ее задают векторным уравнением 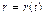 или параметрическими уравнениями:
или параметрическими уравнениями: 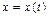 ,
, 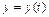 ,
, 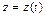 .
.
Дата добавления: 2016-01-26; просмотров: 1447;
