Уравнение линии на плоскости

Уравнение линии на плоскости 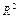задается равенствами: а) в неявном виде 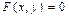, б) разрешенном, относительно y: 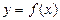, которым удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Переменные х и y в уравнении линии называются текущими координатами точек линии.

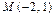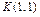Пример V.2. Лежат ли точки и на линии ?

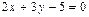Решение.Подставим координаты точки М в уравнение линии: 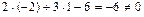– значит, точка М не лежит на заданной линии; теперь подставим координаты точки K: 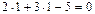– координаты этой точки удовлетворяют уравнению линии, и значит, точка K лежит на заданной прямой.

Задача о нахождении точек пересечения двух линий, заданных уравнениям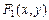и и 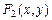, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, то есть сводится к решению системы двух уравнений с двумя неизвестными:

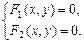
Если эта система не имеет действительных корней, то линии не пересекаются.

Аналогичным образом вводится понятие линии в полярной системе координат. Уравнение 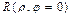называются уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать при помощи двух уравнений:

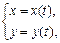
где х, у – координаты произвольной точки 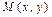, лежащей на данной линии, а t – переменная, называемая параметром линии. Такой способ задания линии называется параметрическим.

Линию на плоскости можно задать и векторным уравнением 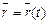, где t – скалярный переменный параметр. Каждому значению 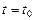соответствует определенный вектор 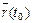на плоскости. При изменении параметра t конец вектора 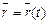опишет некоторую линию.

Векторное и параметрическое уравнения имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линия – траекторией точки, параметр t при этом, интерпретируется как время.

В аналитической геометрии на плоскости возникают две основные задачи: зная геометрические свойства кривой, найти ее уравнение и зная уравнение кривой, изучить ее форму и свойства [4].