Системы координат на плоскости

Под системой координат на плоскости понимают правило, устанавливающее взаимно однозначное соотношение между точками плоскости и упорядоченными парами чисел, которые называют координатами исходной точки.

Проведем через фиксированную на плоскости точку O две несовпадающие прямые с заданными направлениями и единичными отрезками. Если прямые пересекаются под прямым углом, то введенная система координат называется декартовой, или прямоугольной, в противном случае – аффинной, или косоугольной. Первая координата точки в такой системе координат называется абсциссой, вторая – ординатой. Точка пересечения координатных осей называется началом координат.

В декартовой системе координат, обычно, горизонтальную ось Ox называют осью абсцисс, Oy – осью ординат.

Рассмотрим точку M на плоскости Oxy (рис. V.1). Вектор 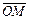называется радиус-вектором точки М. Чтобы найти ее координаты необходимо из этой точки опустить перпендикуляры на каждую из осей. Числа, соответствующие полученным точкам пересечения, и будут координатами точки 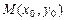. Если точка лежит на оси Ox, то ее вторая координата равна 0, если на оси Oy, то – первая.

Другой практически важной системой координат является полярная. Возьмем на плоскости геометрическую прямую Ox и зафиксируем на ней декартову систему координат Oxy. Начало назовем полюсом, а координатную ось – полярной осью. Рассмотрим произвольную точку M на плоскости. Ее положение будет однозначно определено, если задать расстояние r от начала координат до точки M и угол j, на который нужно повернуть ось Ox вокруг точки O против часовой стрелки до совмещения его направления с отрезком 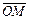(рис. V.1).

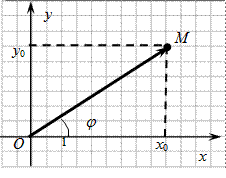
Рис. V.1

Полярными координатами точки M на плоскости называется пара чисел 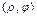. Число r называется полярным радиусом, а число j – полярным углом. Обычно считают, что

, .

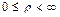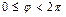Если точка M совпадает с началом, то угол j считается неопределенным.

С каждой полярной системой координат связана декартовая (рис. V.1). Начало совпадает с полюсом, ось абсцисс – с полярной осью, а ось ординат совпадает с полярной осью, повернутой вокруг полюса на угол .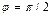

Пусть точка M в декартовой системе координат имеет координаты 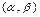, тогда прямая связь с полярными запишется в виде

, .

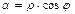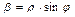Для обратной зависимости имеем соотношения

, ,

, .

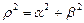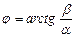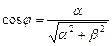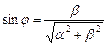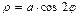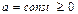Пример V.1. Кривая в полярной системе координат задана уравнением , где . Требуется построить график в полярной системе координат и записать уравнение этой кривой в декартовой системе координат.

Зафиксируем декартову систему координат Oxy и на оси абсцисс зададим полярную ось Ox с одинаковым масштабом с декартовой системой (рис. V.2).

Составим табл. 1 с ценой деления .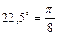

Таблица V.1

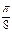
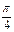
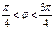
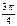
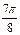
j							p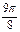
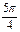
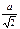
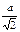
r	a			–			a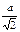
j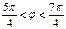
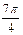
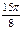
r	–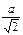

Каждую пару 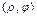на полярной плоскости и соединим плавной кривой, которая называется «двухлепестковой розой». Часто для построения графика достаточно рассмотреть известные значения тригонометрических функций 0, 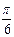, , 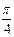, 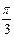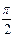и кратные им.

В декартовых координатах двухлепестковая роза с помощью формул перехода записывается уравнением

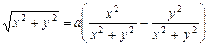
или, после элементарных преобразований, получим

.

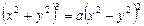Ясно, что в полярной системе координат построение графиков, относящихся к классу подобных кривых, менее трудоемко, чем в декартовой системе координат.

Рис. V.2