Значения hSLD – расстояния по прямой линии до Бухареста
| Обозначение узла | Название города | Расстояние до Бухареста по прямой | Обозначение узла | Название города | Расстояние до Бухареста по прямой |
| Arad | Арад | Pitesti | Питешти | ||
| Bucharest | Бухарест | Rimnicu-Vilcea | Рымнику-Вылча | ||
| Craiova | Крайова | Sibiu | Сибиу | ||
| Fagaras | Фэгэраш | Timisoara | Тимишоара | ||
| Oradea | Орадя | Zerind | Зиренд |
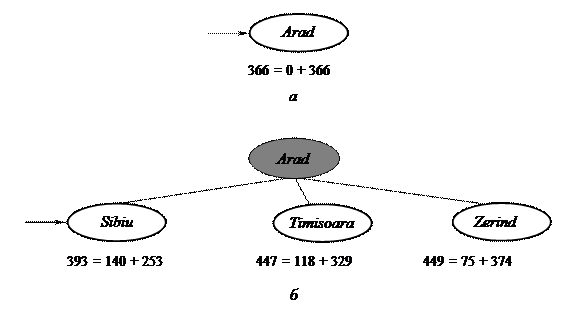
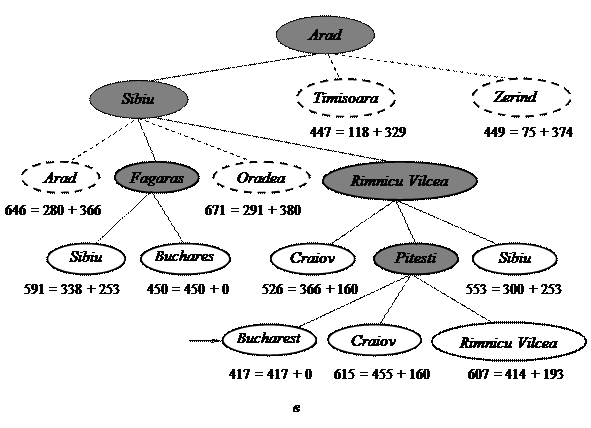
Рис. 32. Этапы поиска A* пути в Бухарест (узлы отмечены значениями f = g + h).
а – начальное состояние; б – после развертывания узла Arad;
в – после последовательного развертывания узлов Sibiu,
Rimnicu Vilcea, Fagaras, Pitesti
Предположим наличие периферийного неоптимального целевого узла G2,а стоимость оптимального решения, равную c*. Поскольку узел G2не оптимален, а для любого целевого узла h(G2) = 0, то справедлива следующая формула:
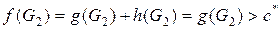 .
.
Рассмотрим периферийный узел 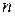 , который находится в оптимальном пути решения, например узел Pitesti (рис. 32, в). Если решение существует, то всегда должен быть такой узел. Если функция h(n) не переоценивает стоимость завершения этого пути решения, то справедливы следующие неравенства
, который находится в оптимальном пути решения, например узел Pitesti (рис. 32, в). Если решение существует, то всегда должен быть такой узел. Если функция h(n) не переоценивает стоимость завершения этого пути решения, то справедливы следующие неравенства
 ,
,
 .
.
Поэтому узел G2не развертывается и поиск A*должен вернуть оптимальное решение.
При организации поиска A*вместо алгоритма «поиск по дереву» иногда используется алгоритм«поиск по графу». Этот алгоритм получается путем модификации алгоритма «поиск по дереву» включением в него структуры данных, называемой «закрытым списком», в котором хранится каждый развернутый узел. (Периферию, состоящую из неразвернутых узлов, иногда называют «открытым списком».) Если текущий узел совпадает с любым узлом из «закрытого списка», то он не развертывается, а отбрасывается. При решении задач со многими повторяющимися состояниями алгоритм «поиск по графу» является более эффективным по сравнению с алгоритмом «поиск по дереву».
Вопрос о том, оптимален ли поиск по этому алгоритму, остается сложным. Если вновь обнаруженный путь короче первоначального, то алгоритмом « поиск по графу» при использовании поиска по критерию стоимости предусмотрено отбрасывание наиболее дорогостоящего из любых двух найденных путей к одному и тому же узлу. Сопровождение необходимой для этого дополнительной информации связано с определенными трудностями, но гарантирует оптимальность.
Решение проблемы надежности поиска пути по этому алгоритму состоит в обеспечении того, чтобы оптимальный путь к любому повторяющемуся состоянию всегда был первым из всех возможных, как в случае поиска по критерию стоимости. Для обеспечения этого на функцию h(n) налагается дополнительное требование гарантийной преемственности эвристической функции (такое свойствоназывают также монотонностью эвристической функции). Преемственность имеет место, если для любого узла n и для любого его преемника n', сформированного в
результате любого действия a,оценка стоимости достижения цели из
узла n не больше, чем стоимость этапа достижения узла n'плюс оценка стоимости достижения цели из узла n':
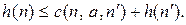
Если представить себе треугольник, образованный узлами n, n' и целевым узлом, ближайшим к узлу n,то приведенное неравенство будет соответствовать характерному для треугольника правилу: длина любой стороны треугольника не может превышать сумму длин двух других сторон.
По аналогии с контурами равных высот на топографических картах могут быть очерчены контуры равных f-стоимостей в пространстве состояний (рис. 33), т. е. все узлы внутри контура имеют значения £ f(n). При поиске по критерию стоимости A* и соблюдении условия h(n) = 0 контуры будут представлять собой «кольца» с центром в начальном состоянии. С использованием более точных эвристических функций полосы становятся более вытянутыми и сосредоточенными в направлении целевого состояния. Для поиска A* первоначальноиз концентрической полосы с наименьшейстоимостью выбирается периферийный узел с минимальной f-стоимостью, далее процесс поиска повторяется для узлов из полос с возрастающей стоимостью. Поскольку целевые узлы во всех последующих контурах имеют более высокое значение f-стоимости и, соответственно, более высокое значение g-стоимости (для всех целевых узлов h(n) = 0), первое найденное решение является оптимальным. Если стоимость оптимального пути решения равна C*, то процесс поиска A* сопровождается:
· развертыванием всех узлов со значением f(n) < C*;
· развертываниемнекоторых дополнительных узлов, находящихся непосредственно на «целевом контуре», где f(n) < C*, прежде чем будет выбран целевой узел.
Требование полноты поиска A*обеспечивается при конечном количестве узлов со стоимостью £ C*; это условие соблюдается, если стоимости всех этапов превышают некоторое конечное значение e, а коэффициент ветвления b является конечным.
Необходимо отметить, что в поиске A*узлы со значением f(n) > C*
не развертываются в связи с отсутствием необходимости их исследования. Например, как показано на рис. 32, несмотря на то, что узел Timisoara является дочерним узлом корневого узла, он не развертывается и происходит отсечение поддерева, находящегося ниже этого узла. Поскольку функция hSLD является допустимой, рассматриваемый алгоритм может игнорировать это поддерево.
Рассмотренный алгоритм поиска A* является оптимально эффективным для конкретной эвристической функции. Однако он не гарантирует развертывание меньшего количества узлов с помощью иного оптимального алгоритма, если не считать выбора на равных среди узлов с f(n) = C*. Это обусловлено тем, что любой алгоритм, который не развертывает все узлы со значениями f(n) < C*, подвержен риску потери оптимального решения.
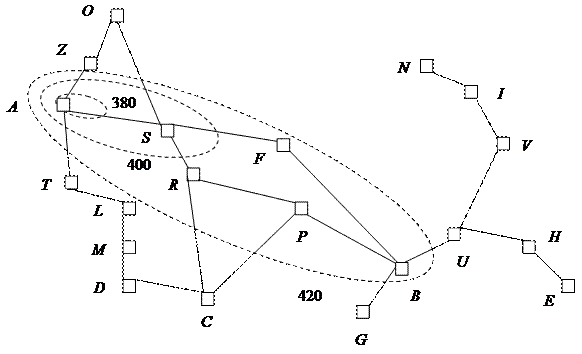
Рис. 33. Контуры стоимости расстояний на карте Румынии (f = 380, f = 400, f = 420,
при условии, что Arad является начальным состоянием)
Не смотря на то, что алгоритмы подобные поиску A*, которыеразвертывают пути от корня, являются действительно полными, оптимальными и оптимально эффективными, это отнюдь не означает, что поиск A*может служить ответом на все потребности в поиске. При решении большинства задач сложность заключается в том, что количество узлов в пределах целевого контура пространства состояний все еще зависит экспоненциально от длины решения. Поэтому в одних случаях целесообразно использовать варианты поиска A*, позволяющие быстро находить
неоптимальные решения, а в других – разрабатывать эвристические функции, которые являются более точными и, хотя не являются строго допустимыми 
 , иногда обеспечивают поразительную экономию усилий по сравнению с использованием неинформационного поиска.
, иногда обеспечивают поразительную экономию усилий по сравнению с использованием неинформационного поиска.
Помимо продолжительности вычислений при реализации алгоритма поиска A* необходимо правильно оценивать требуемый объем памяти. Поиск A* не является практически применимым при решении многих крупномасштабных задач, поскольку в этих случаях все имеющиеся ресурсы памяти, необходимые для хранения сформированных узлов, часто исчерпываются до момента, когда выбираются ресурсы времени. Для преодоления проблемы пространства разработаны специальные алгоритмы, обеспечивающие при относительно небольшом увеличении времени оптимальность и полноту решения задач.
Дата добавления: 2016-01-20; просмотров: 1068;
